Regiomontanus' Problem

Thinking about the best place on earth to observe the rings of Saturn, Regiomontanus posed this problem:
Where on earth does a vertically suspended bar appear to be biggest?

Thinking about the best place on earth to observe the rings of Saturn, Regiomontanus posed this problem:
Where on earth does a vertically suspended bar appear to be biggest?
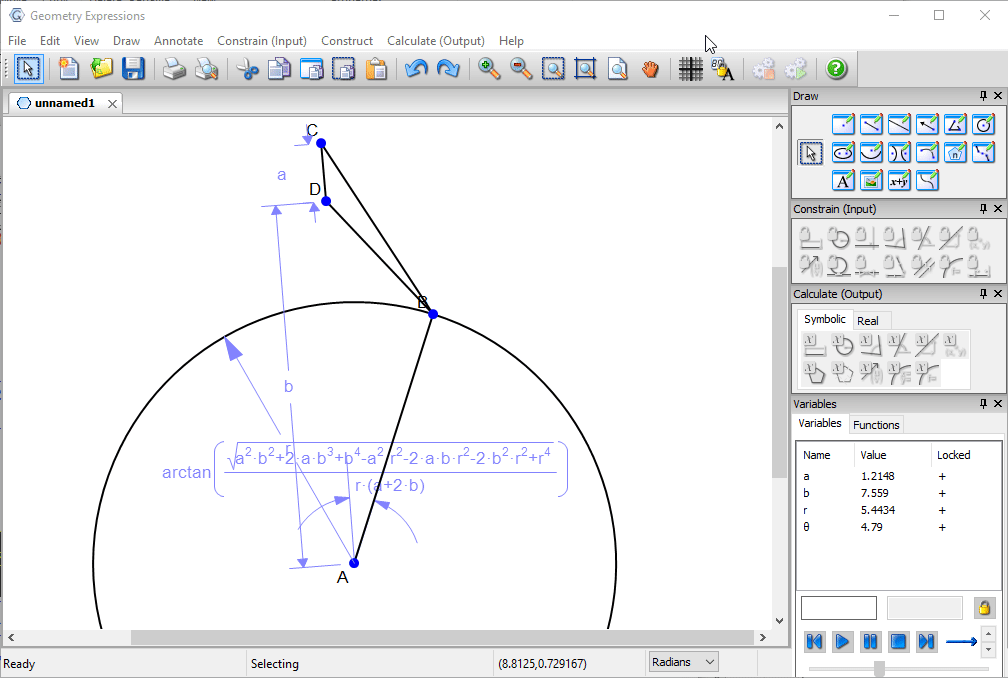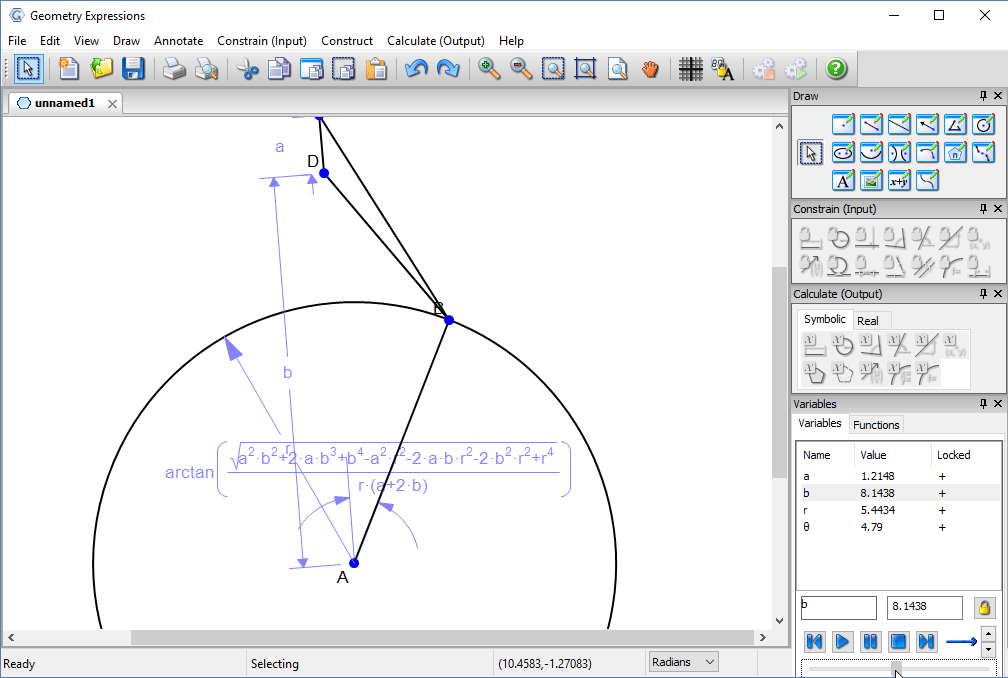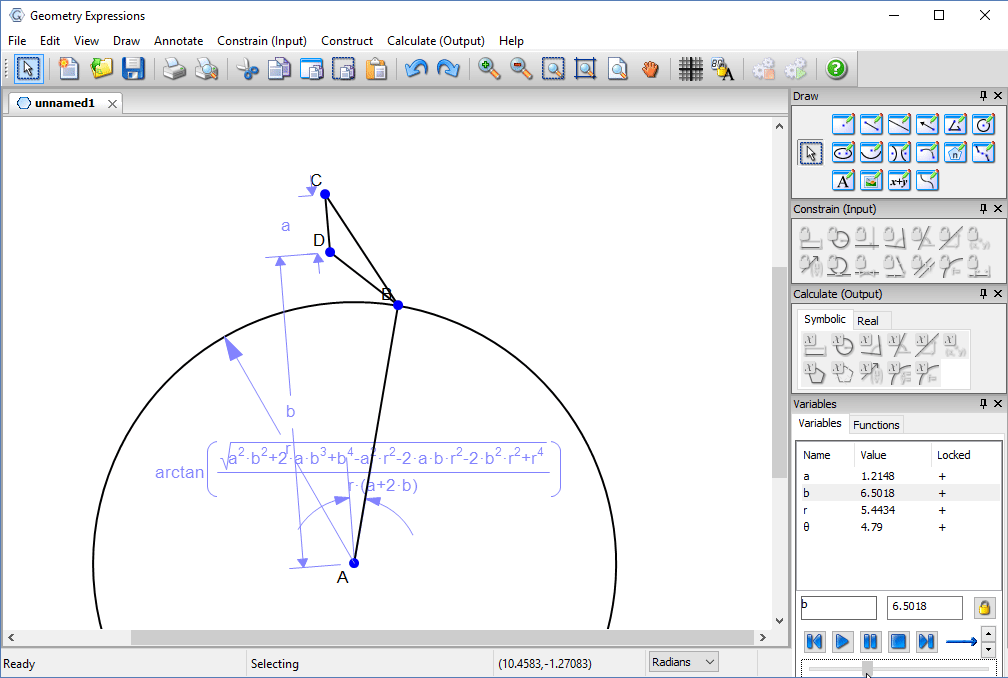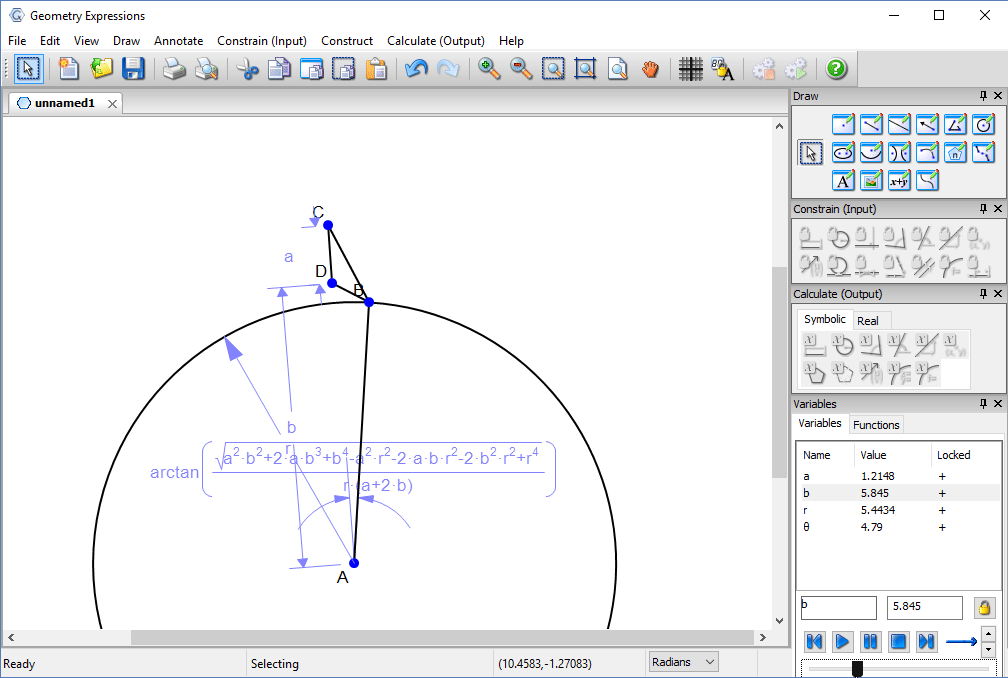
A mathematical model consists of a circle representing the earth, a line segment representing the bar and an observation poin from which lines are drawn to the end of the bar.
The objective will be to find the location on the circle which maximizes the angle subtended by the bar.
We first constrain the center of the circle to lie on the line of the bar.
We then constrain the length of the bar, its height above the center of the earth, and the radius of the earth.
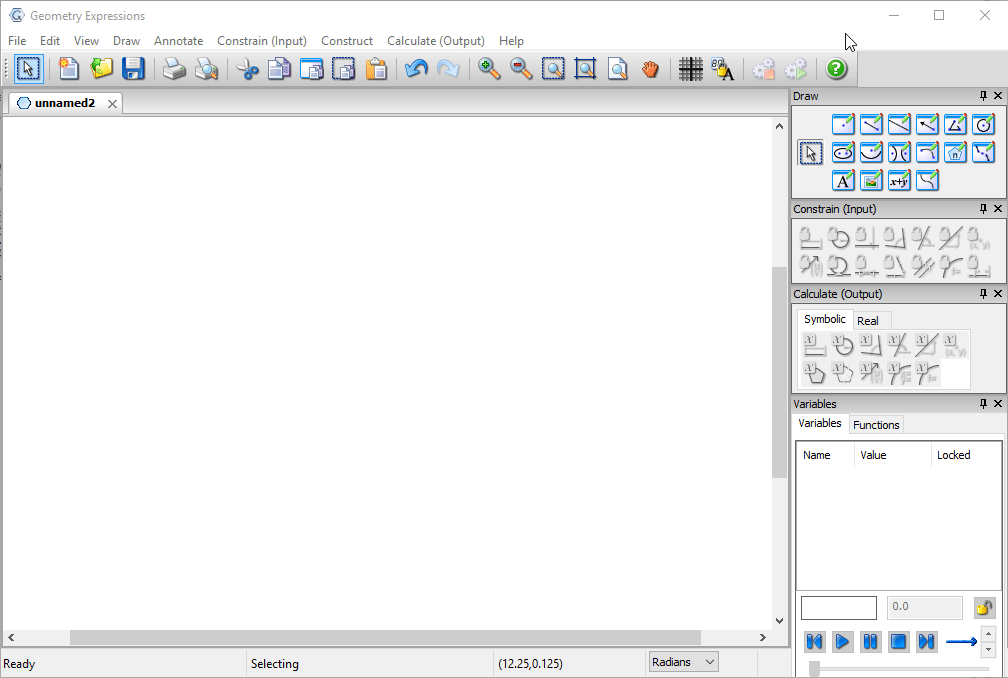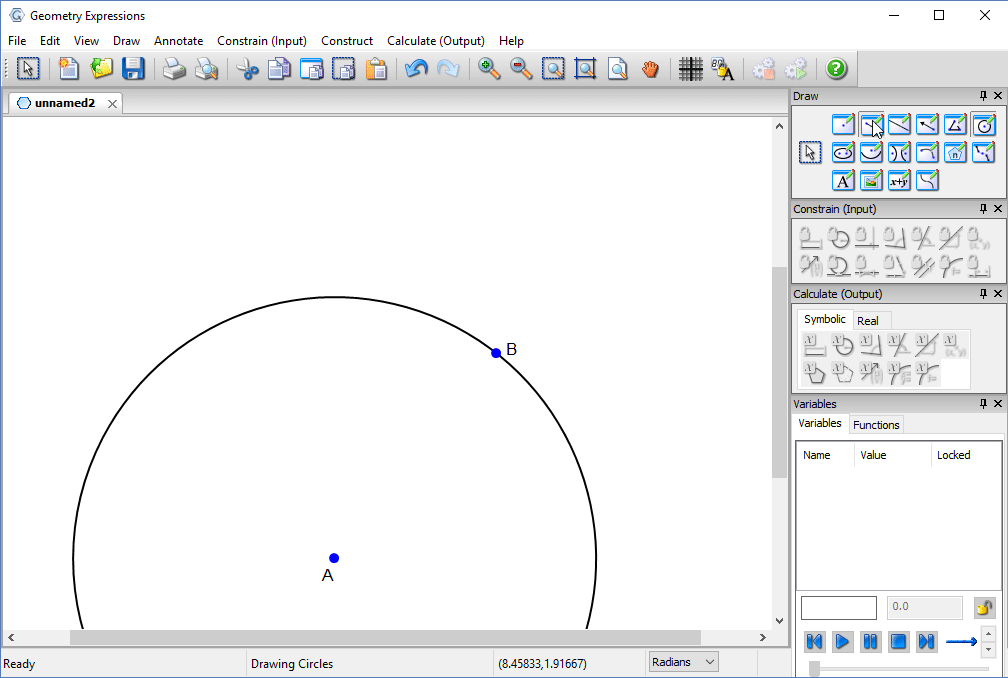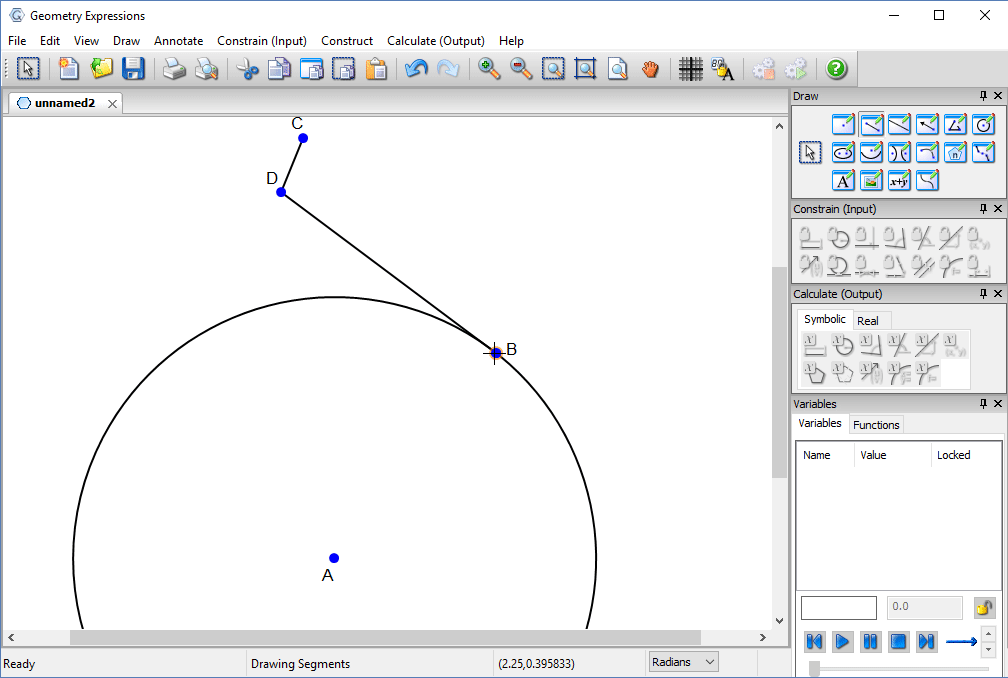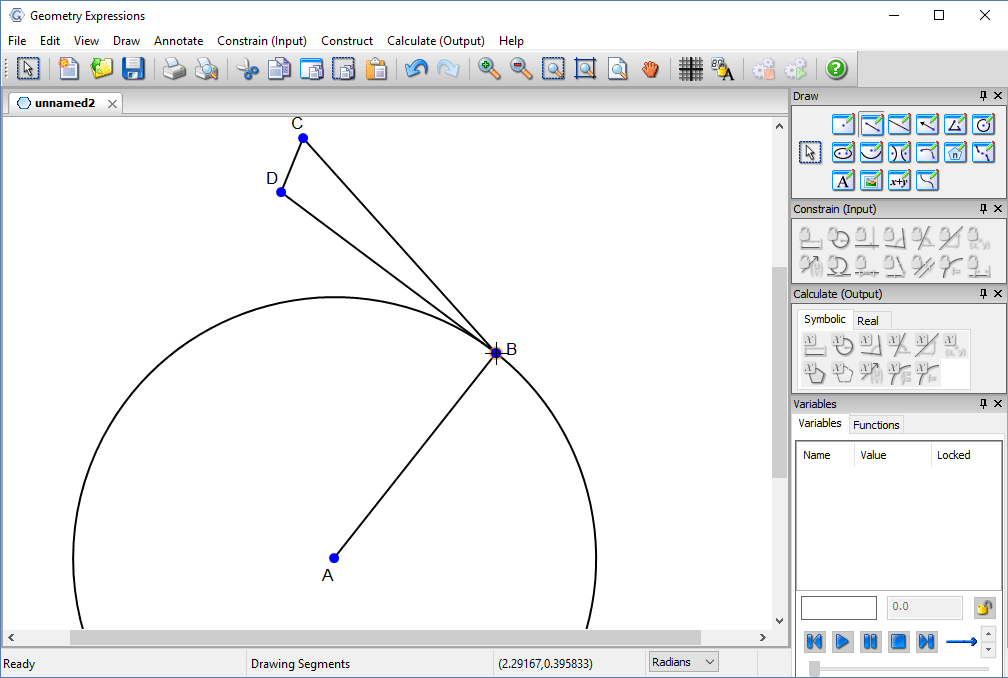
Finally, we specify the angle between the line of the bar and the direction of the observation point. This is our variable x.
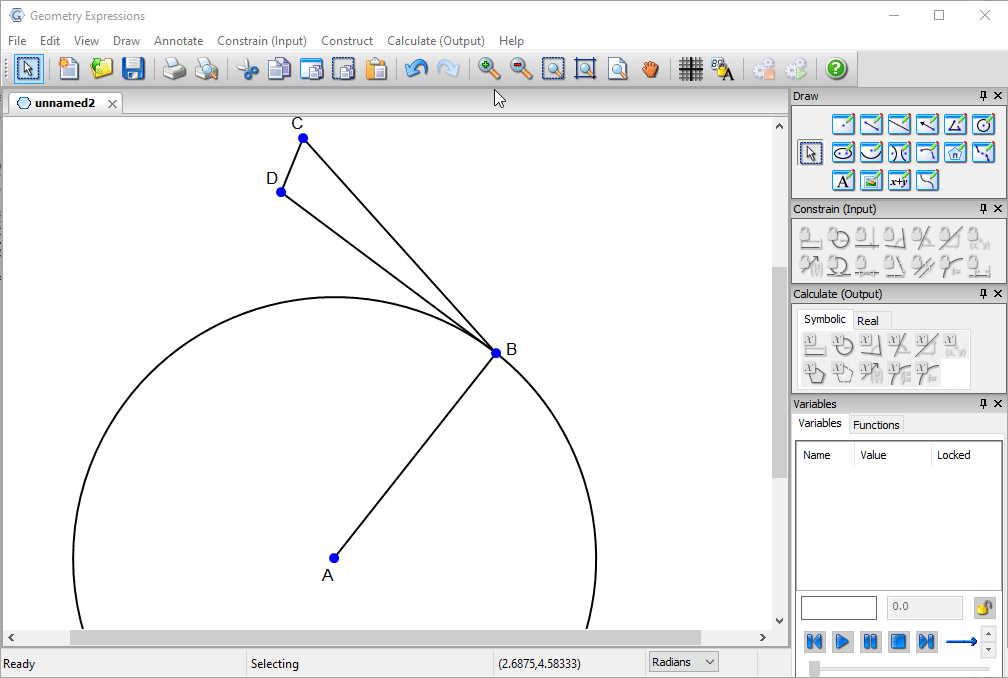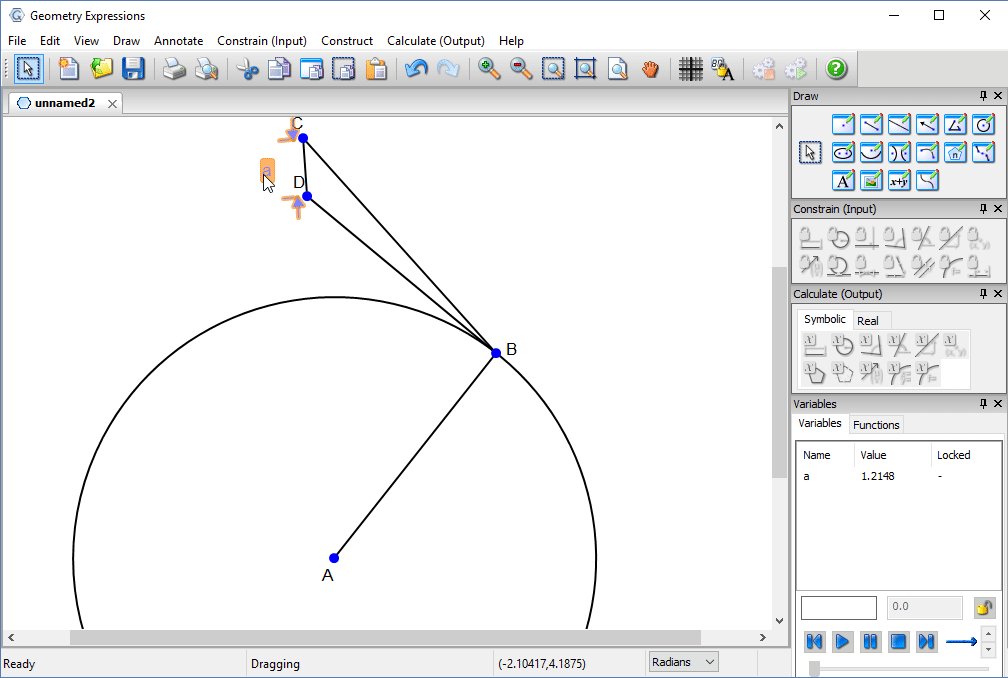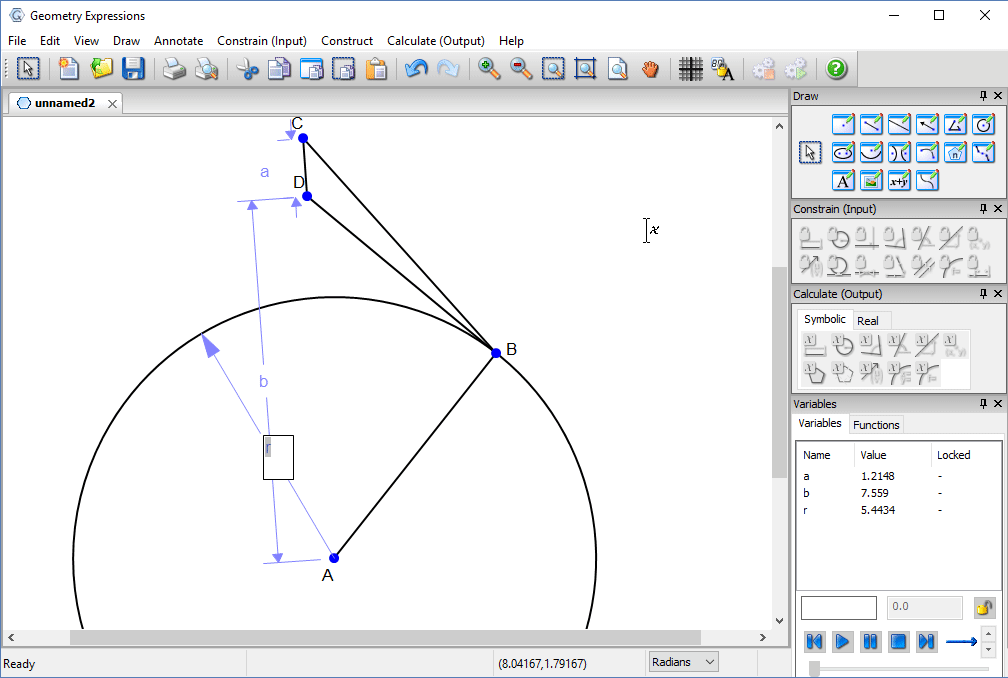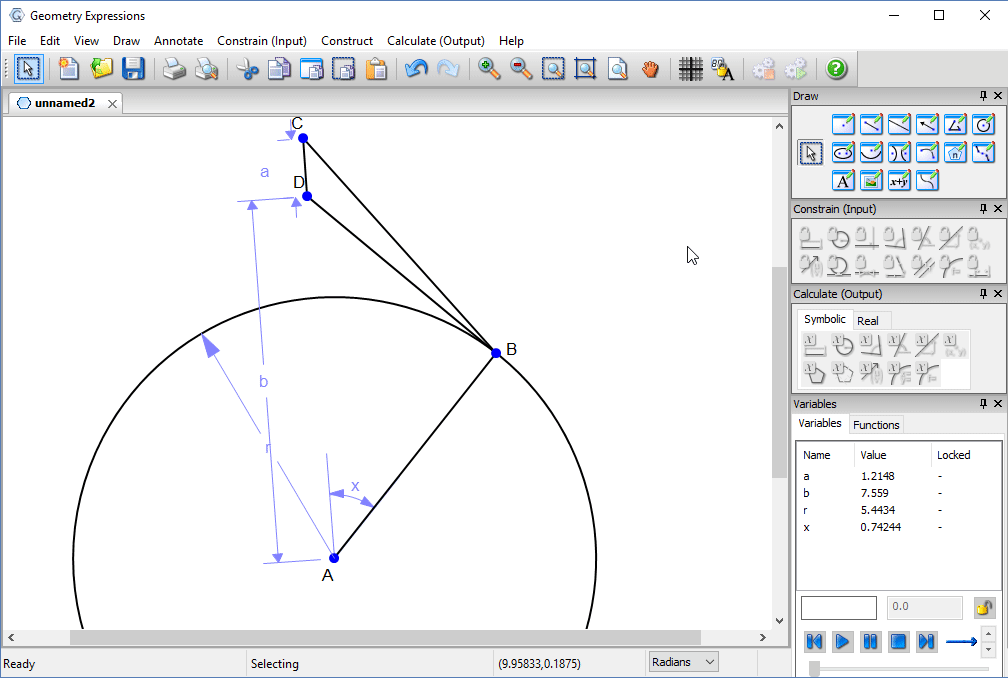
We measure the angle CBD and copy it in a form which we can paste into our CAS.
Whatever CAS you have, one of our formats is likely to work.

We can paste into a CAS, differentiate and solve, then copy the solution.
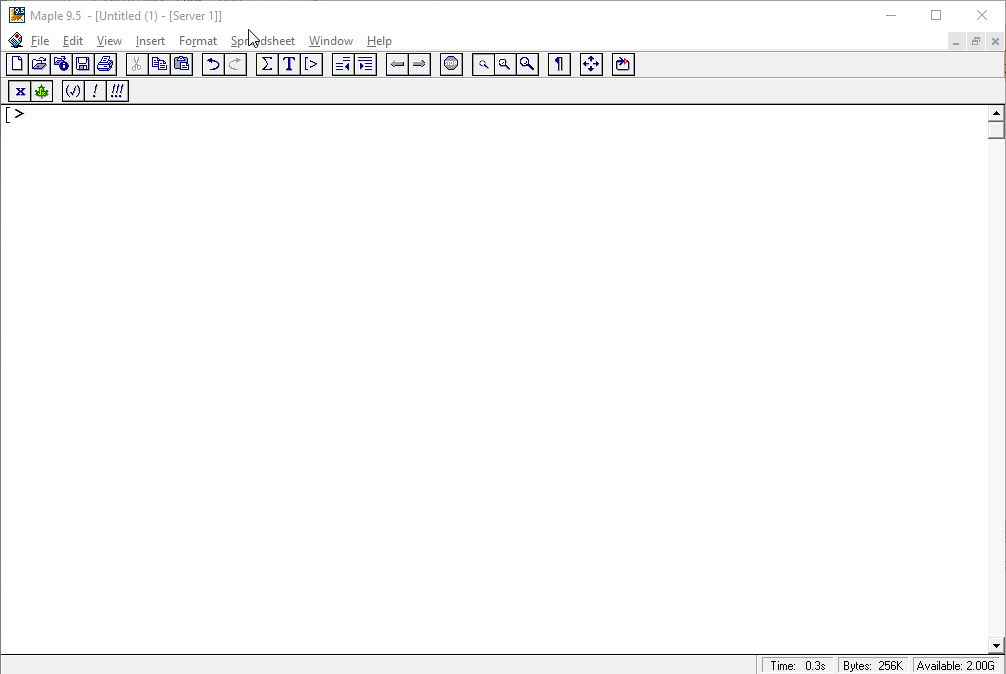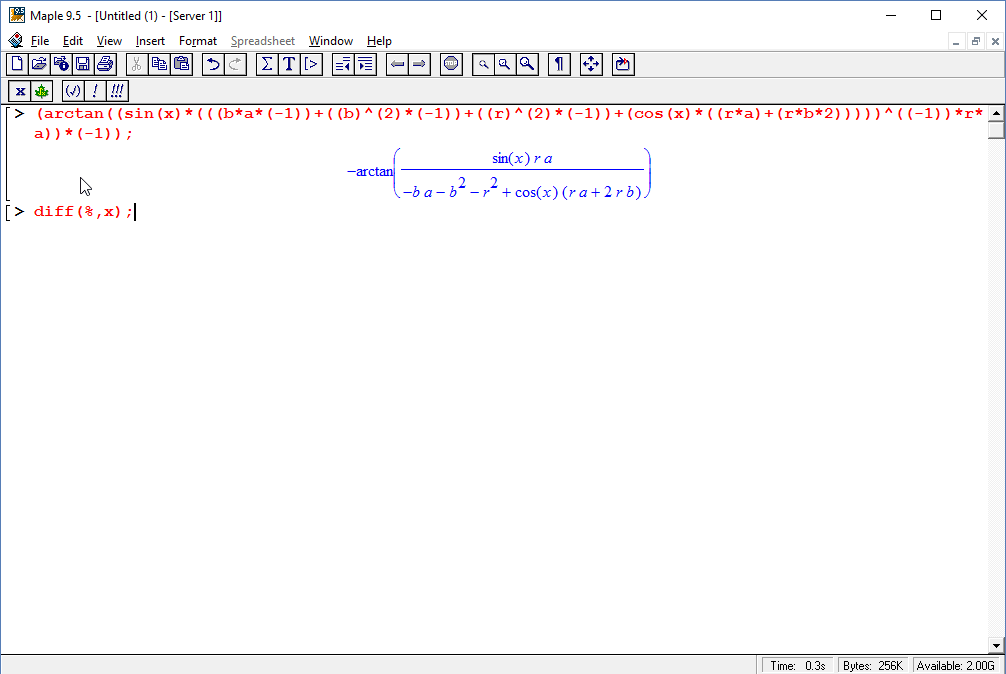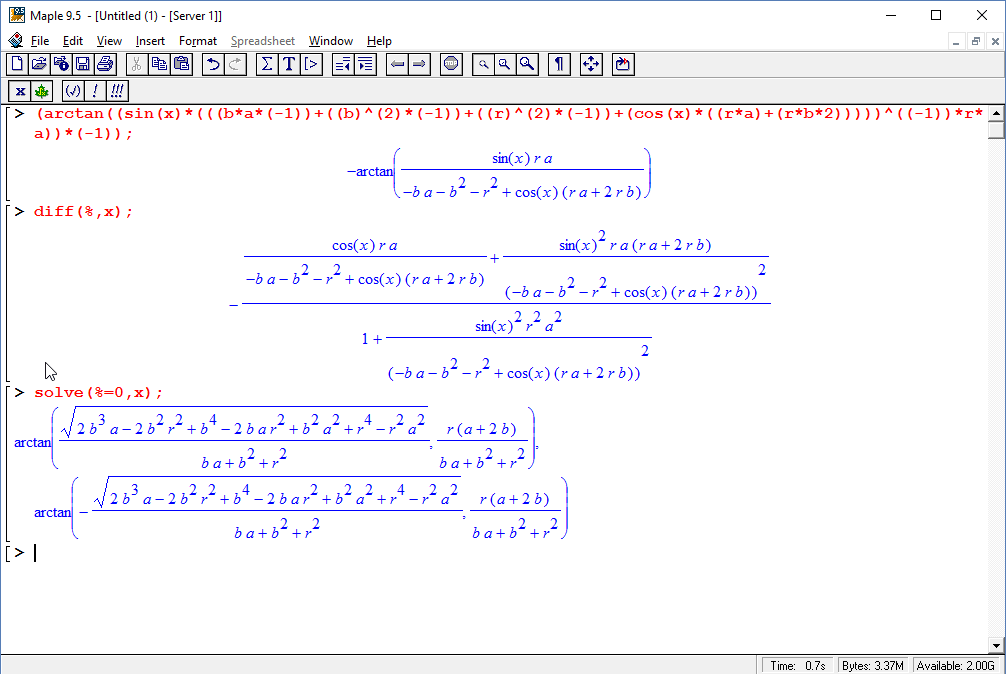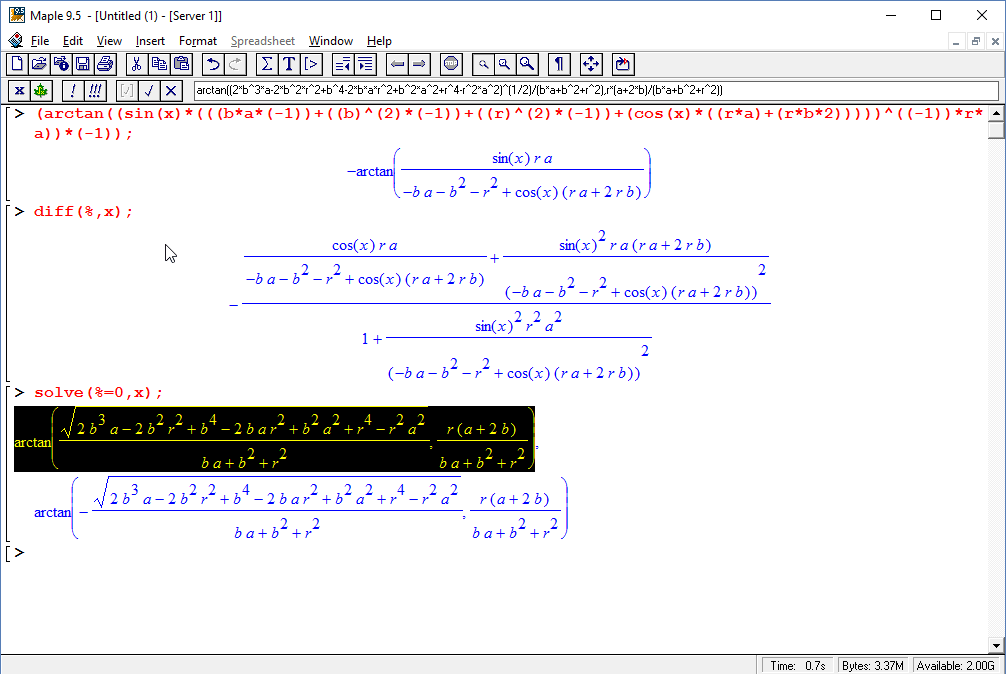
Pasting the solution back into Geometry Expressions provides a useful check (and computes the resulting angle).

We can also traverse the solution space. Here we vary the height of the bar b and observe the effect on the solution.