Some Geometry Theorems

We show how to use GXWeb to prove some geometry theorems.

Theorem 1

Let ABC be a triangle with the angle at B twice the angle at C. Show that the distance between the midpoint of BC and the foot of the altitude from A is half the length of the side AB.

Theorem 2

Let D and E be two points on two sides AC and BC of triangle ABC such that AD=BE. F is the intersection of DE and AB. Show that FD∙AC = EF∙BC

Theorem 3

If a quadrilateral ABCD has opposite sides AD and BC (extended) meeting at E, while F and G are the midpoints of the diagonals AC and BD, then the area of ABCD is 4 times the area of the triangle EFG.

Theorem 4

Let ABCD be a quadrilateral such that AB=CD. E and F are the midpoints of the diagonals and G and H are the midpoints of AD and BC. Show that GH is perpendicular to EF.

Theorem 5

Let E and F be the midpoints of the diagonals of the trapezoid ABCD. Then PQ is parallel to the parallel sides of ABCD and its length is half the difference between the parallel sides.

Theorem 6

On the two sides AB and AC of triangle ABC, two squares ABDE and ACFG are drawn externally. Show that EG is twice the median from A.

Theorem 7

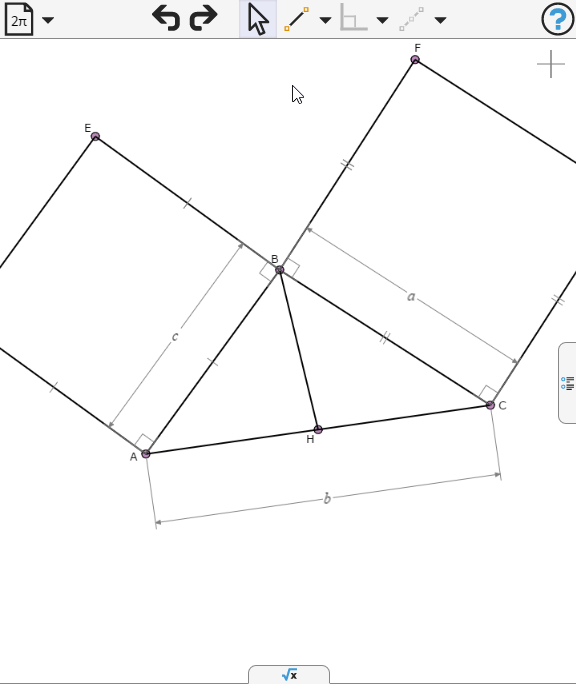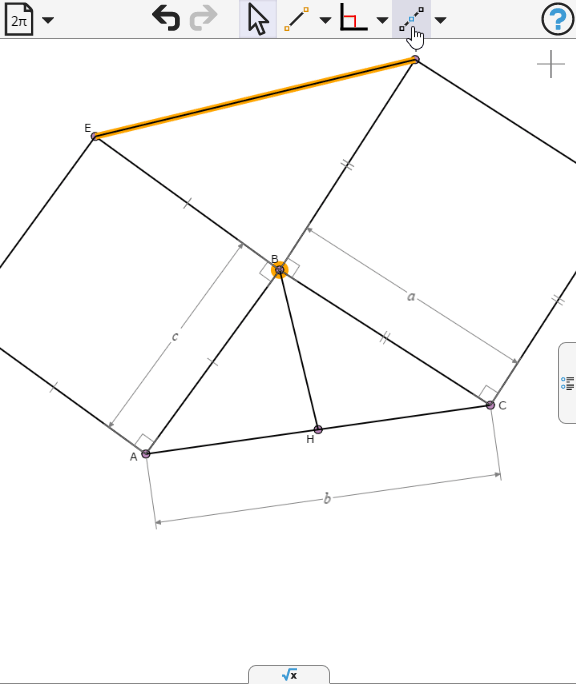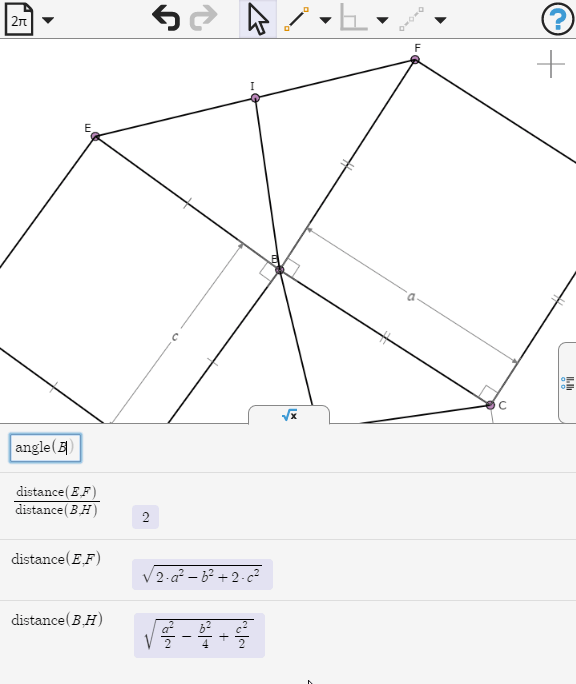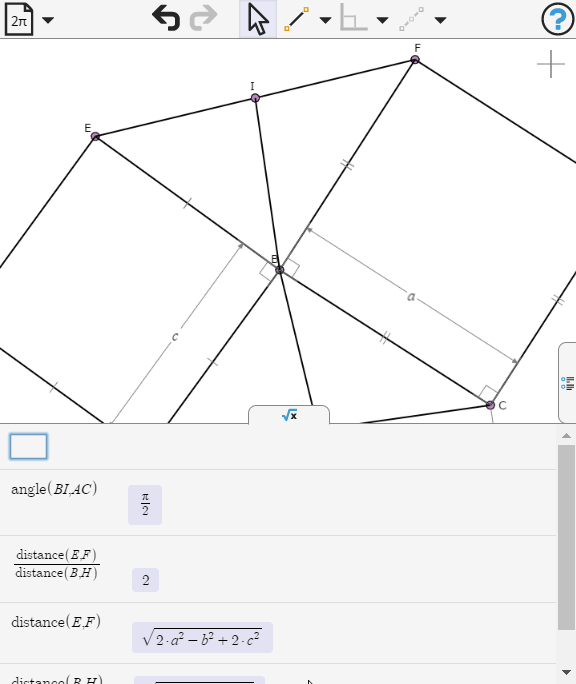
On the Previous diagram, a line passing through A perpendicular to BC touches EG at I. Show I is the midpoint of EG.

Theorem 8

In the Cyclic quadrilateral BCDE, the perpendicular to CD at C meets BE at F, and the perpendicular to BE at E meets CD at F. Show that EF is parallel to BD