When is a spline not a spline?

We look for conditions such that a cubic spline is actually a parabola

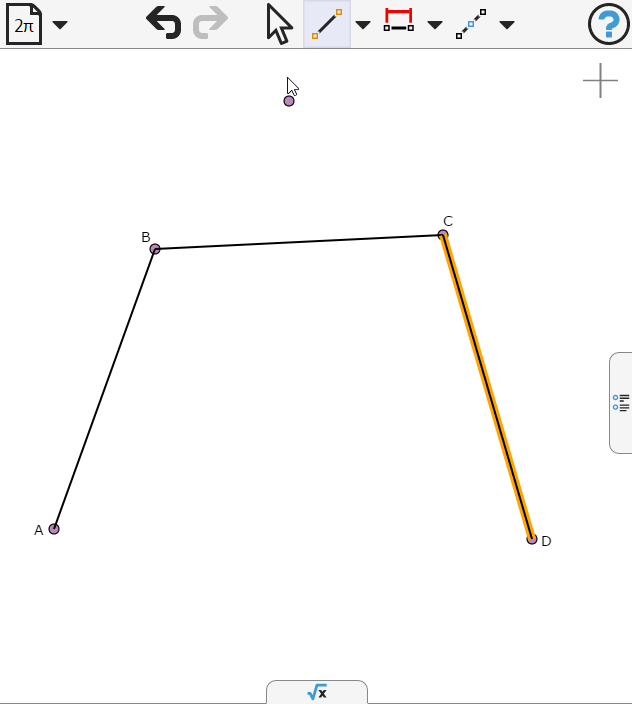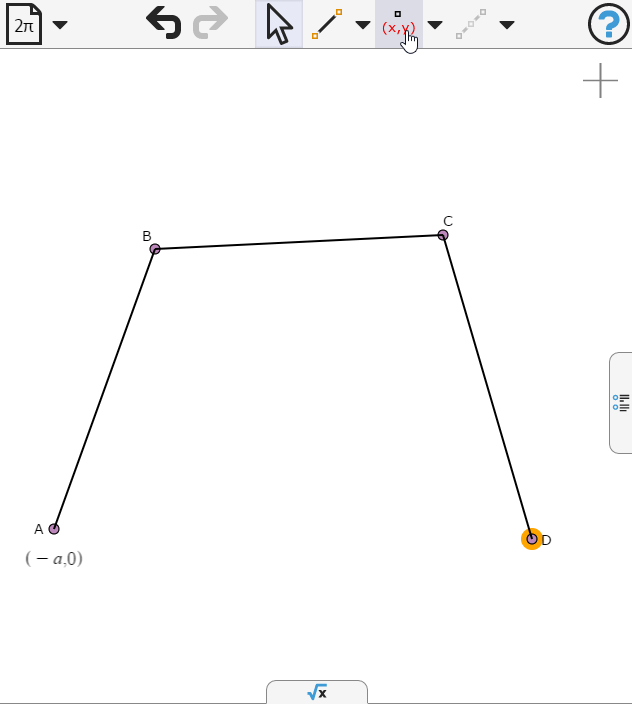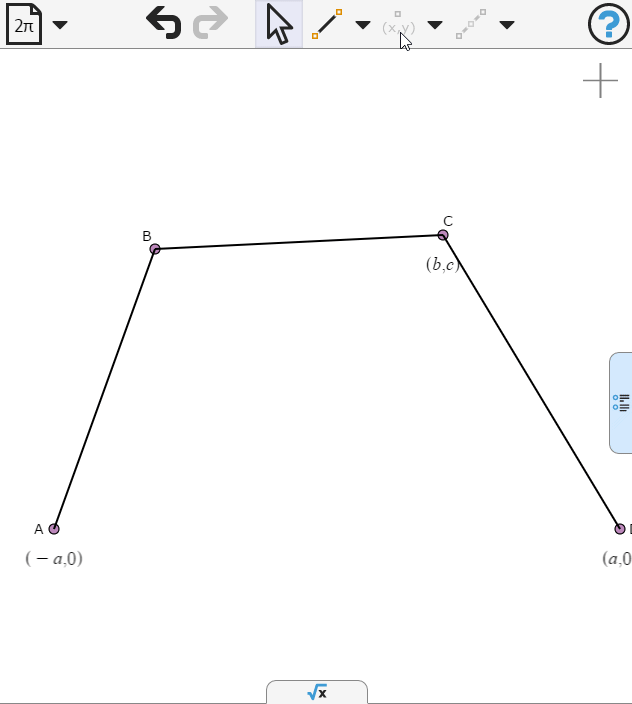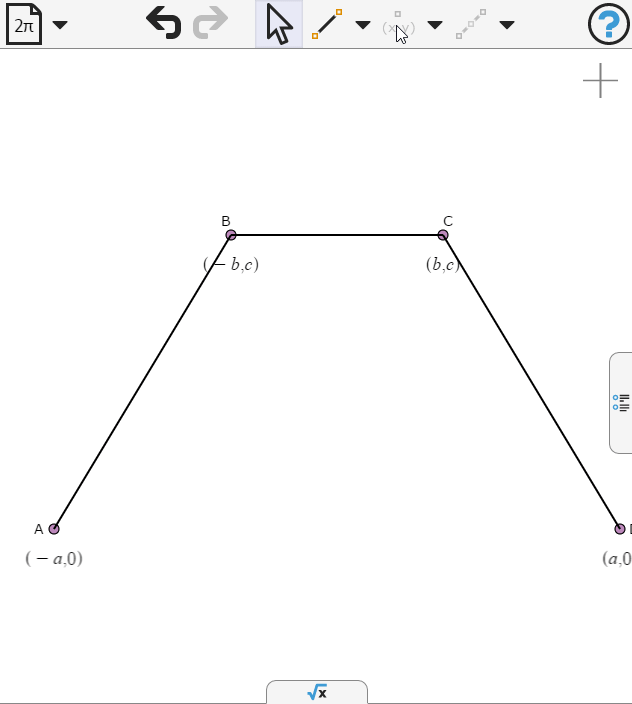
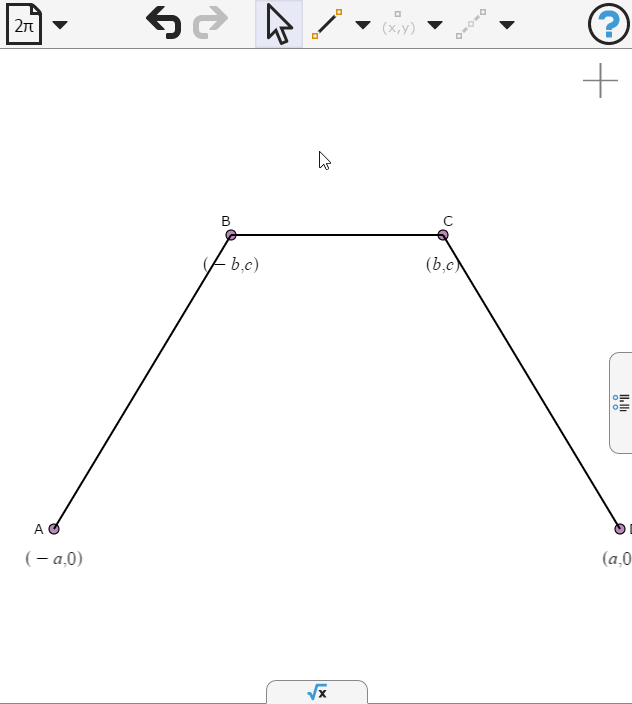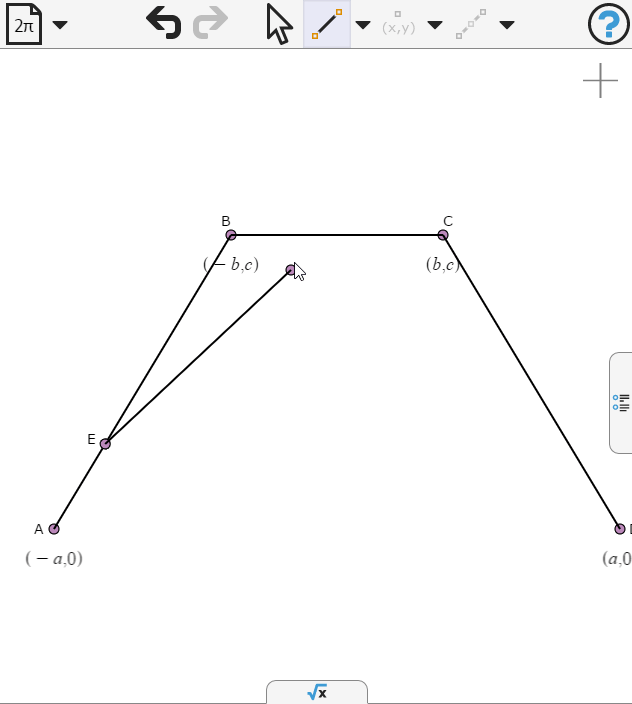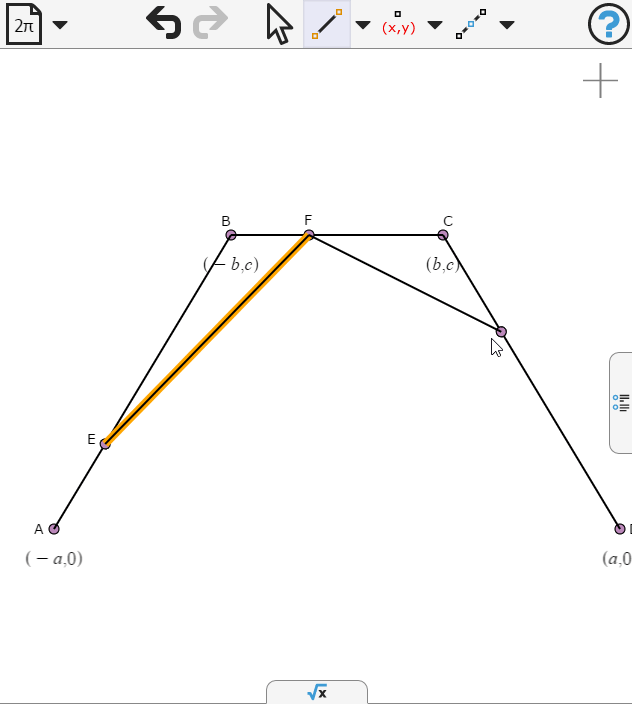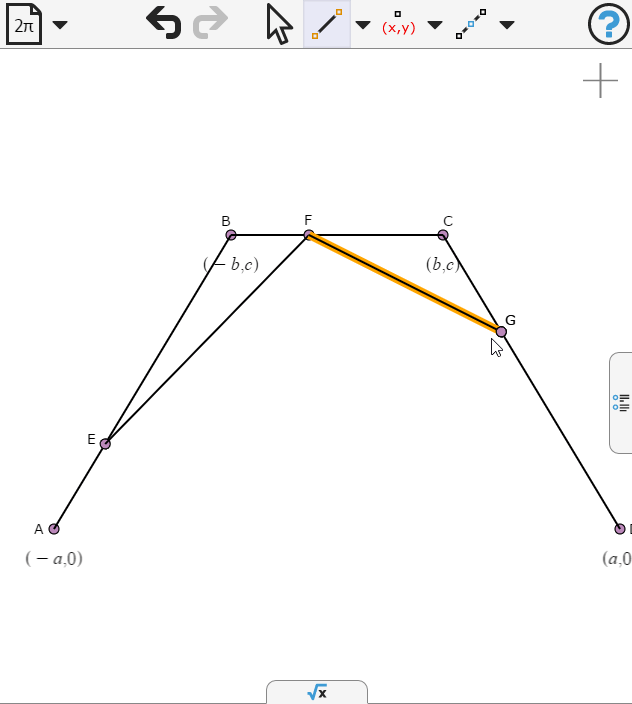
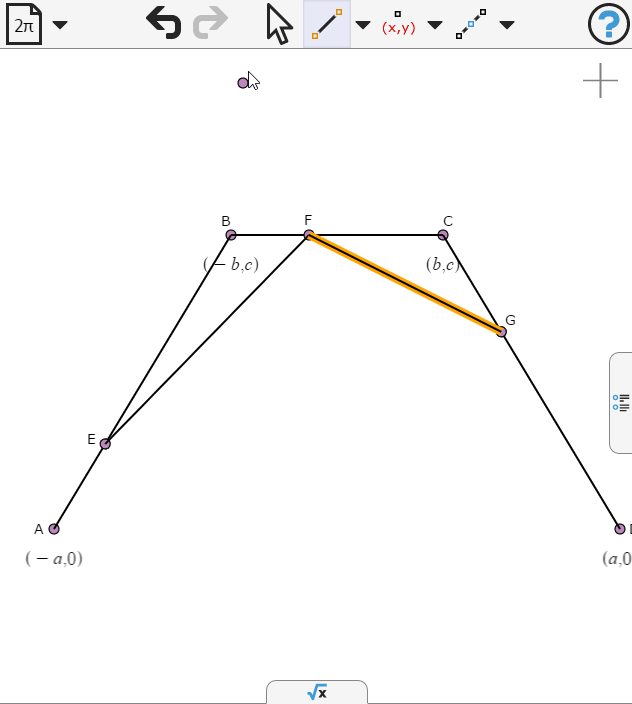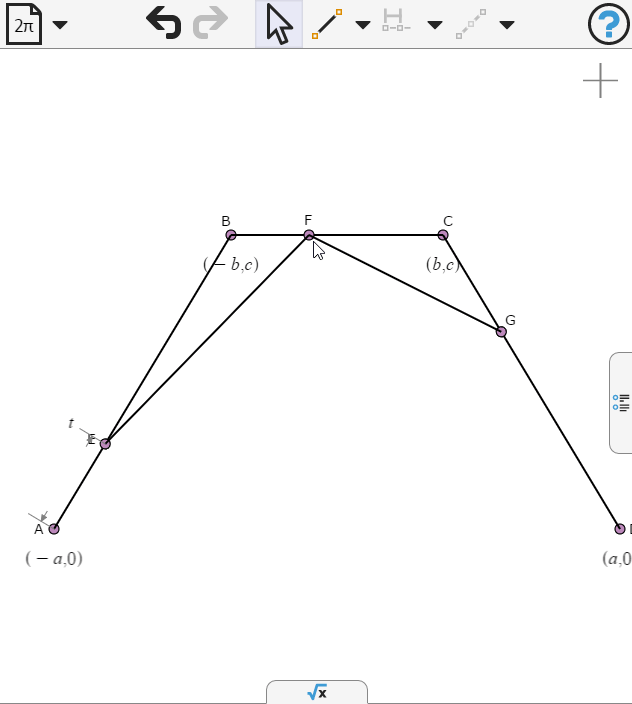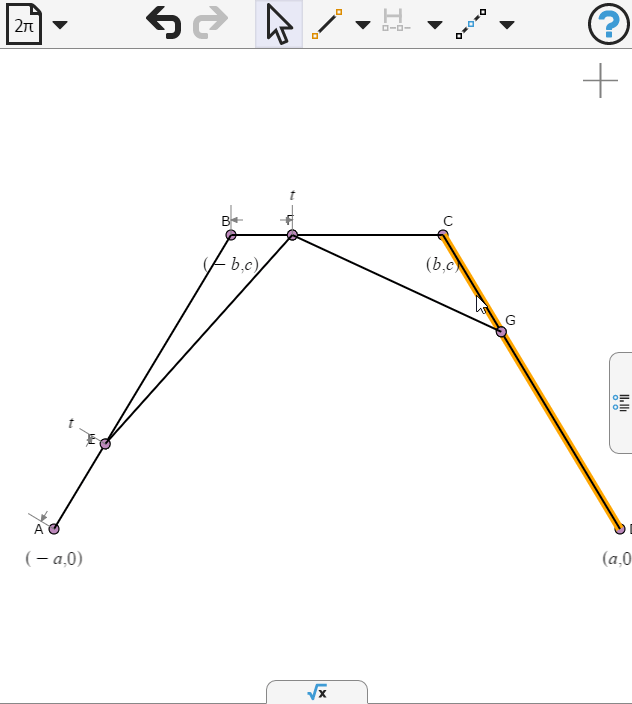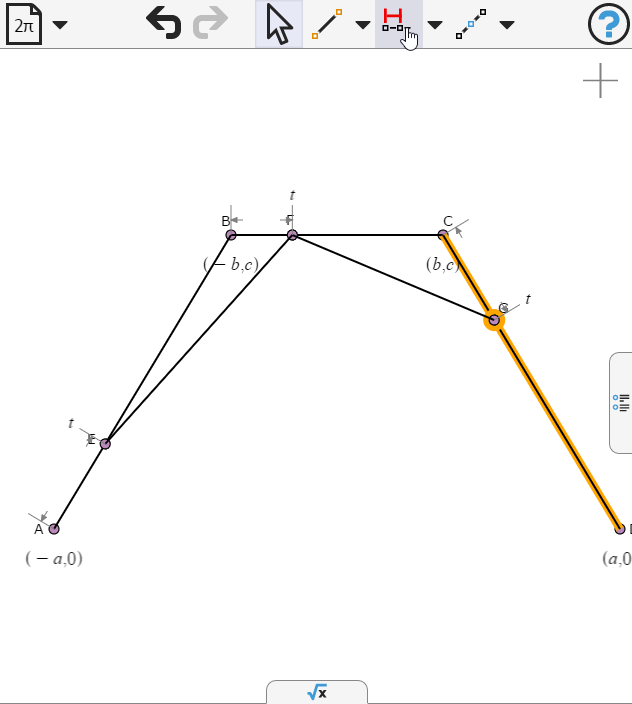
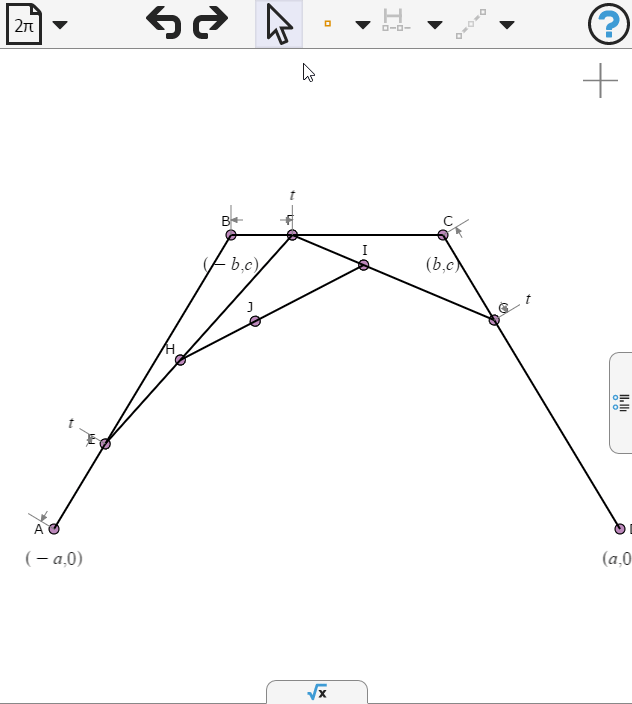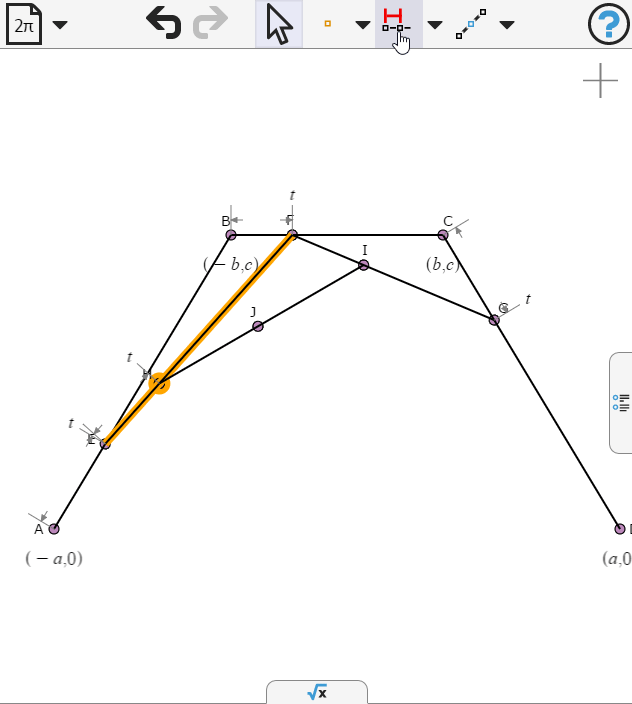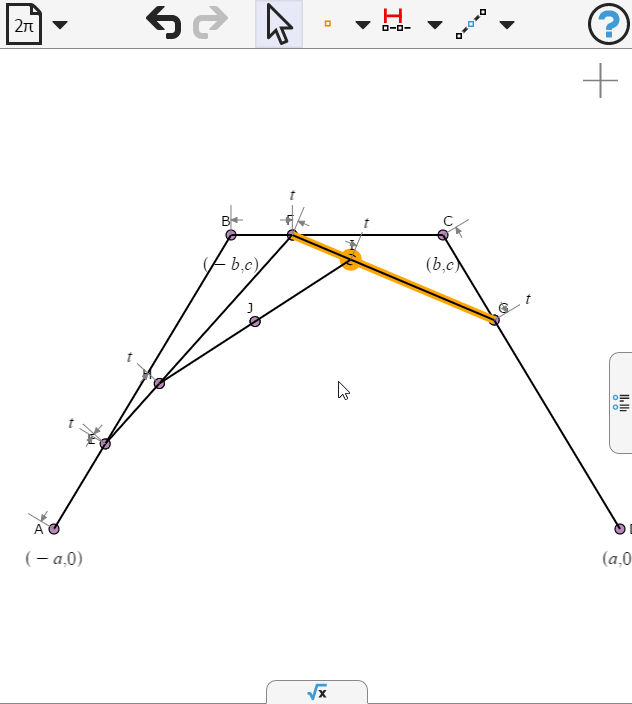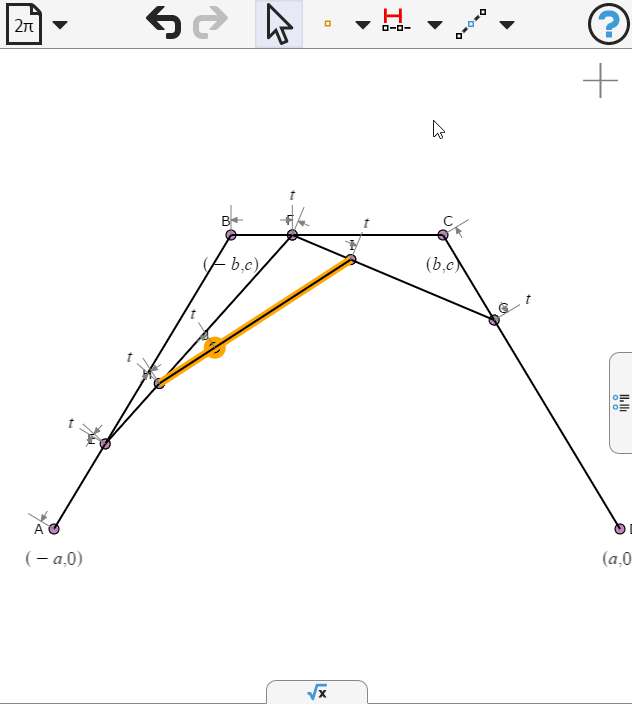
First we draw three sides of the bounding polygon of the spline

We'll set the coordinates of the vertices so that they are symmetric about the y-axis, and two of them lie on the x-axis.

Now we draw two lines which will help in the spline definition.

We define the end points to be propotion t along the respective segments

We draw another segment and place a point on it.

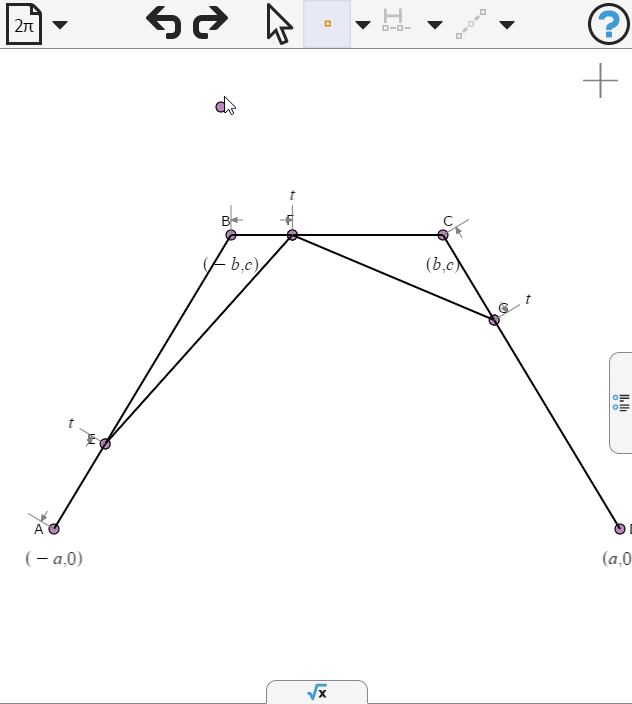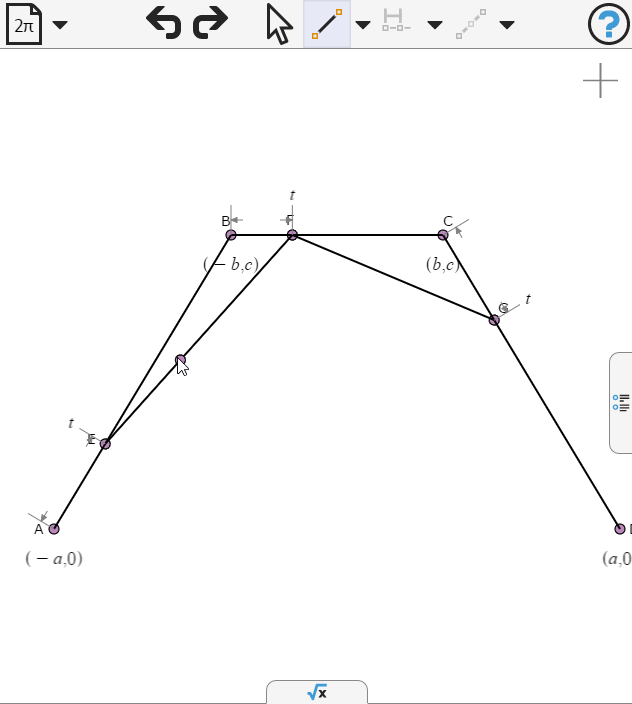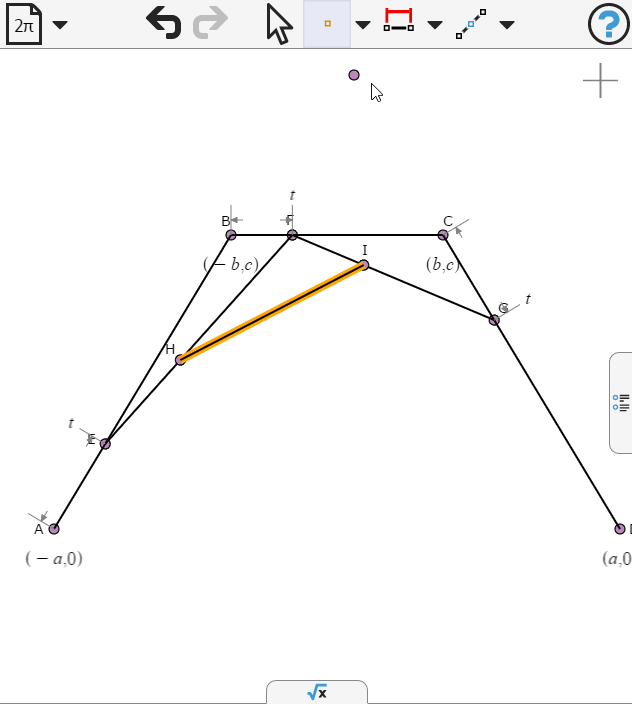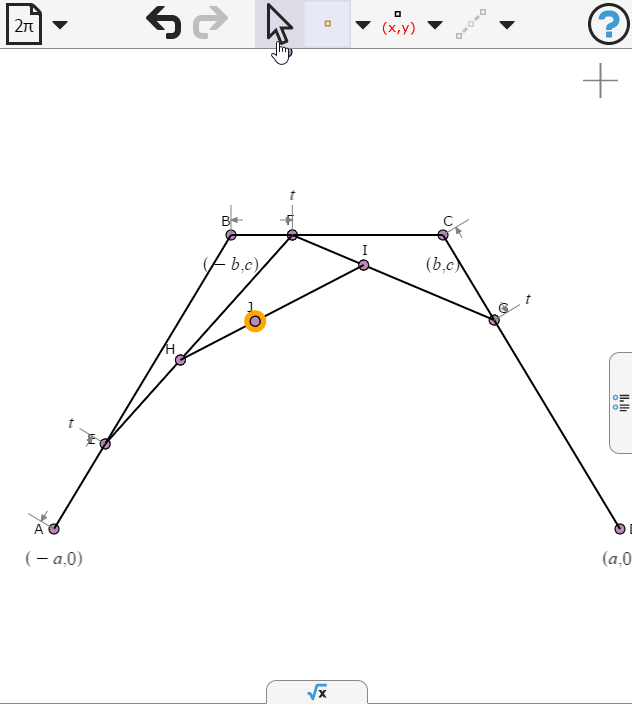
Again we specify the points to be propotion t along the respective segments

We select the last point and create a locus as t varies

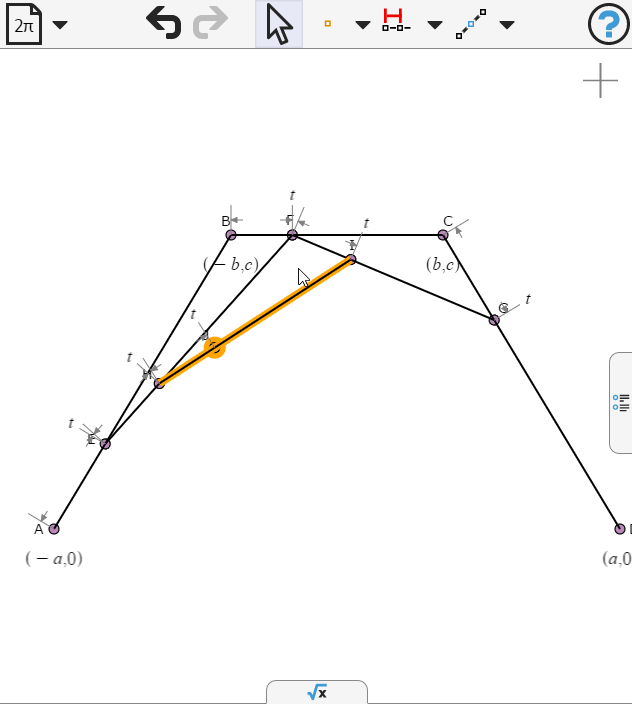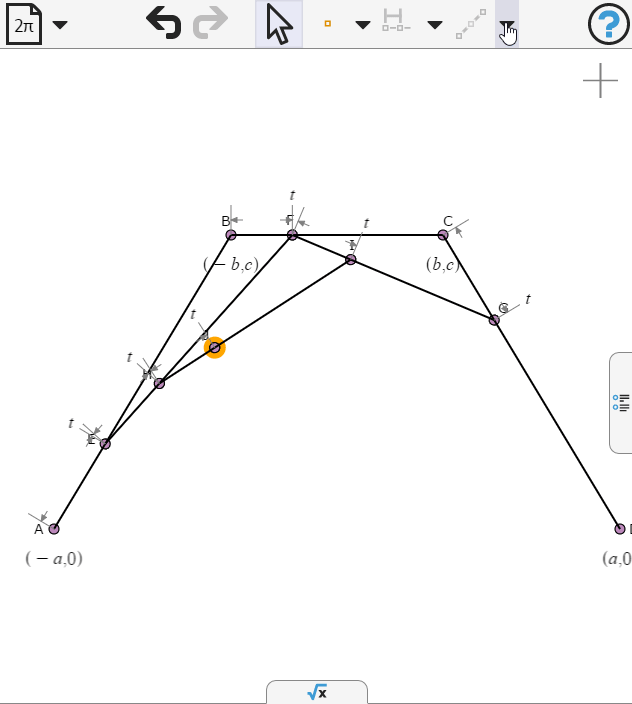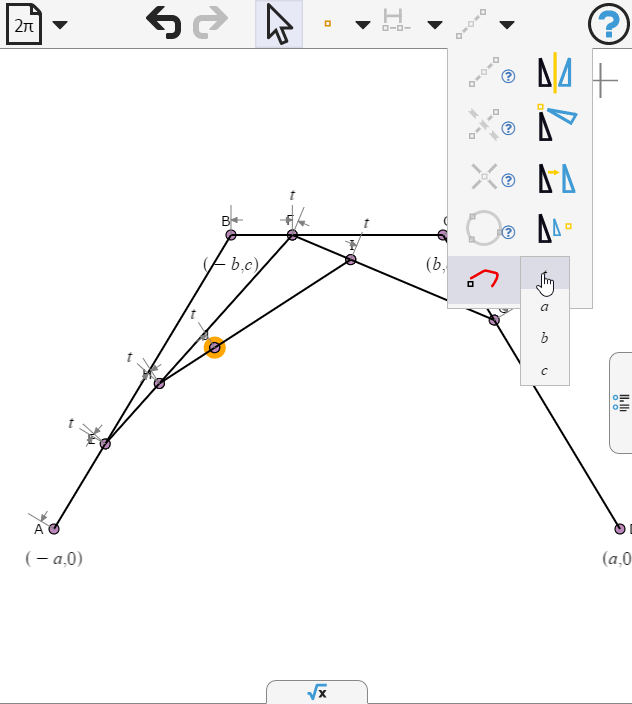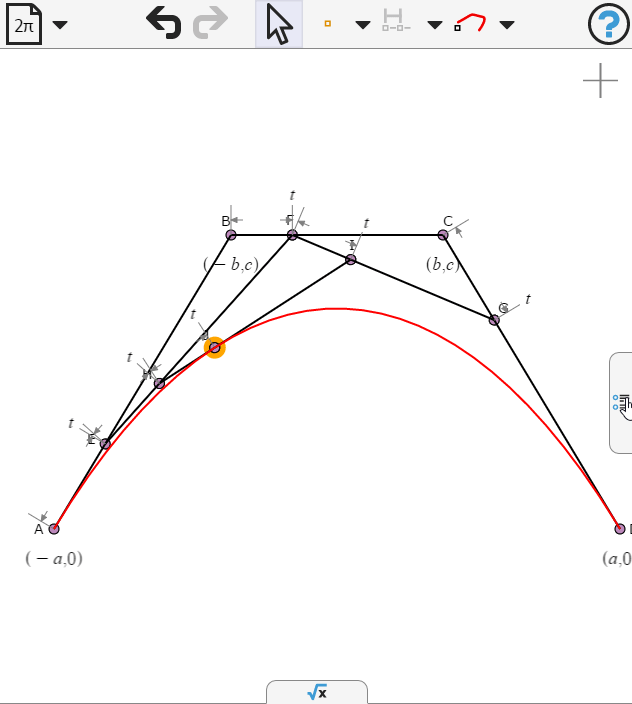
Opening the numeric panel we can animate t

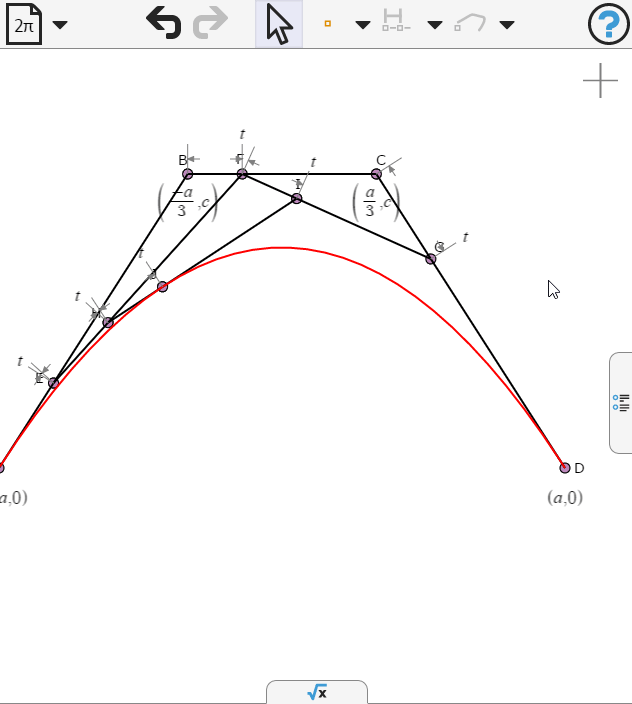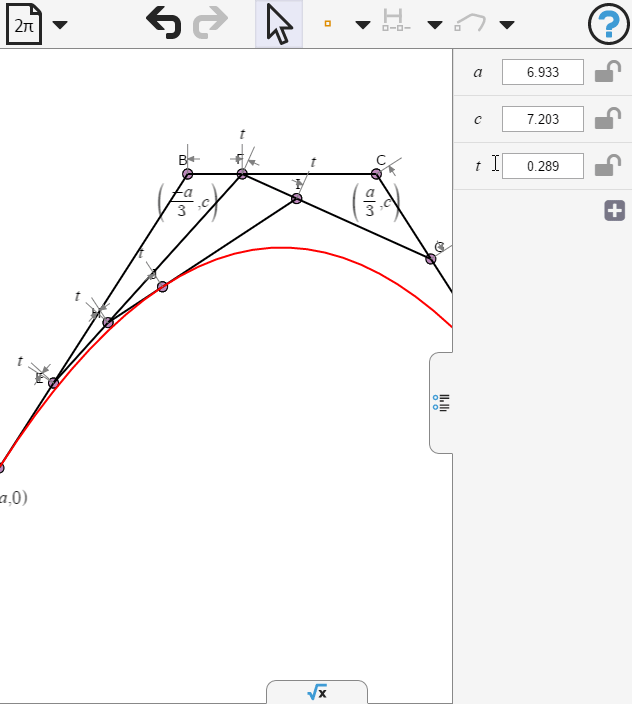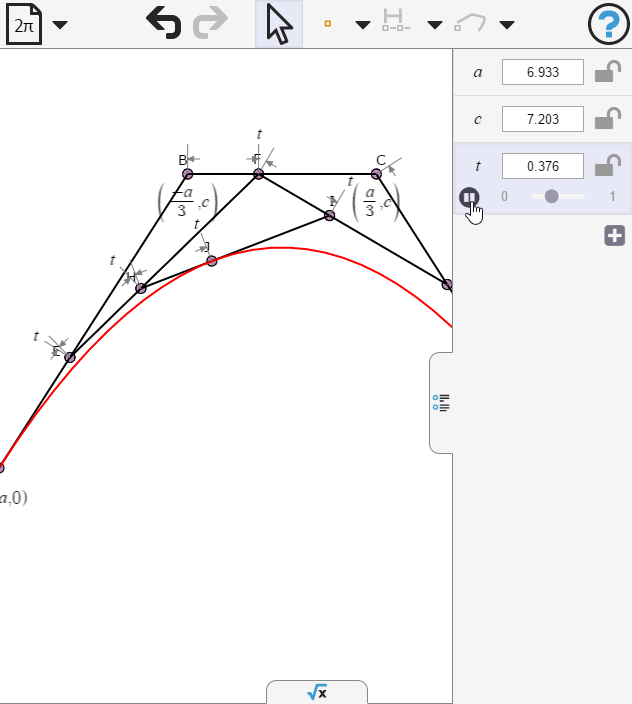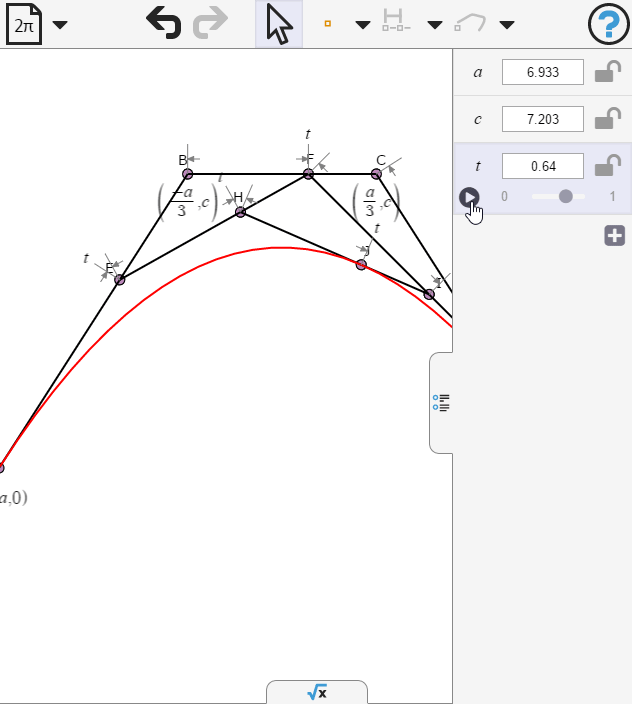
Opening the symbolic panel we can examine the parametric equations of the curve. What value of b would make the cubic terms vanish?

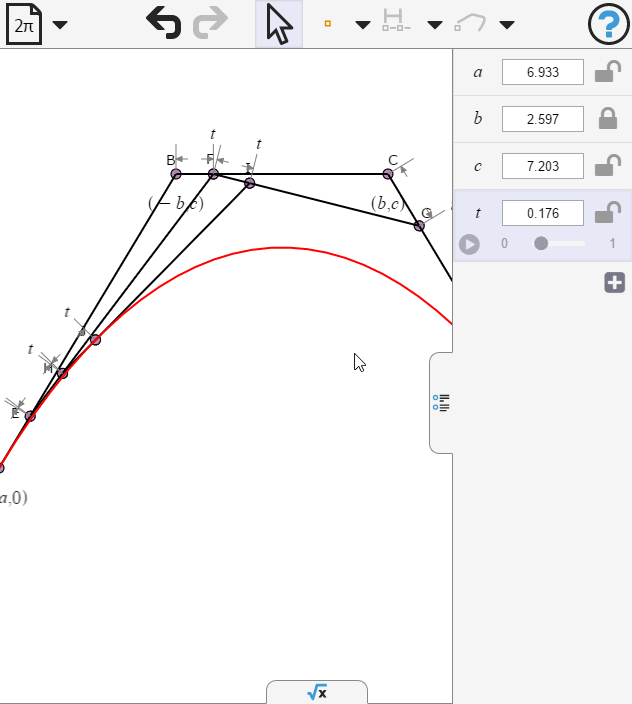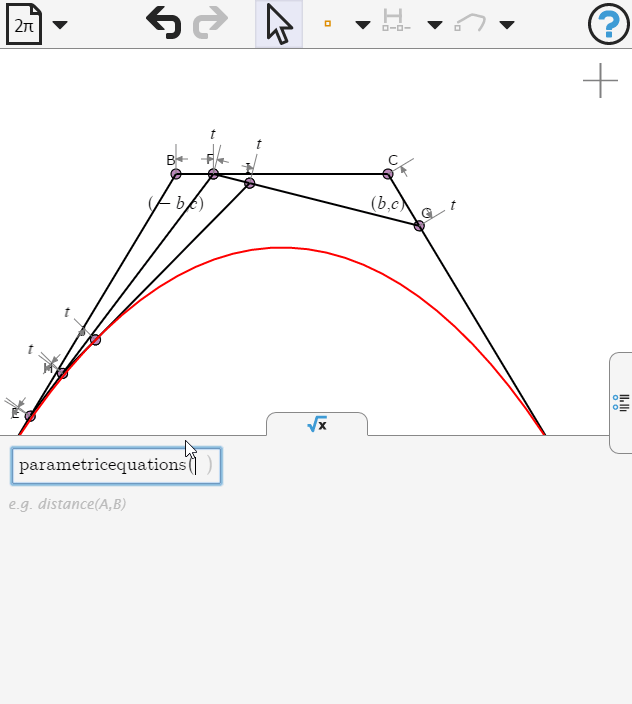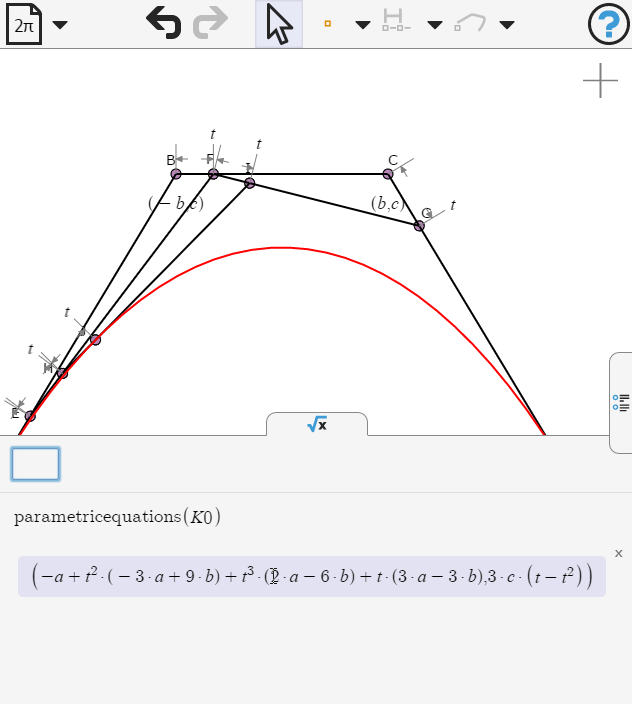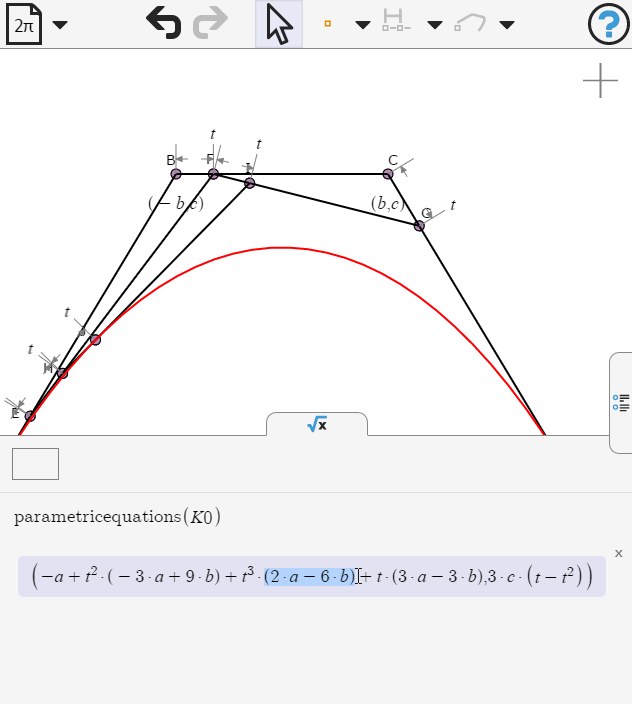
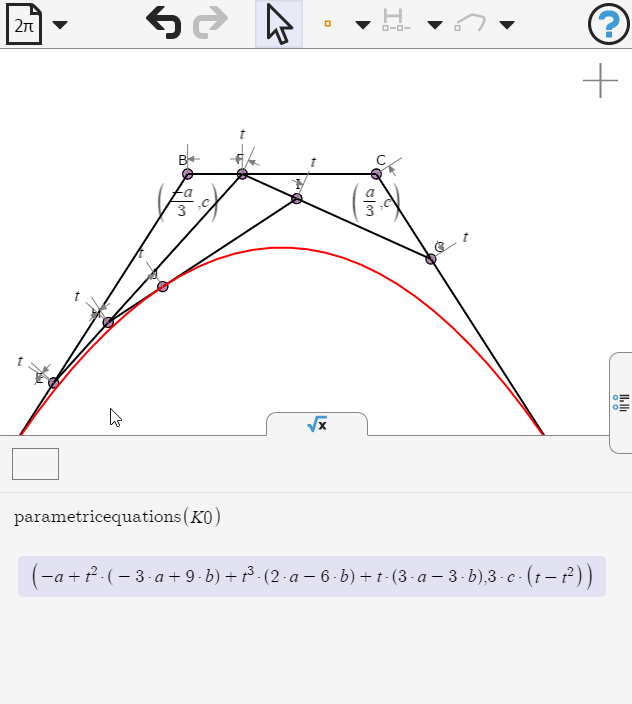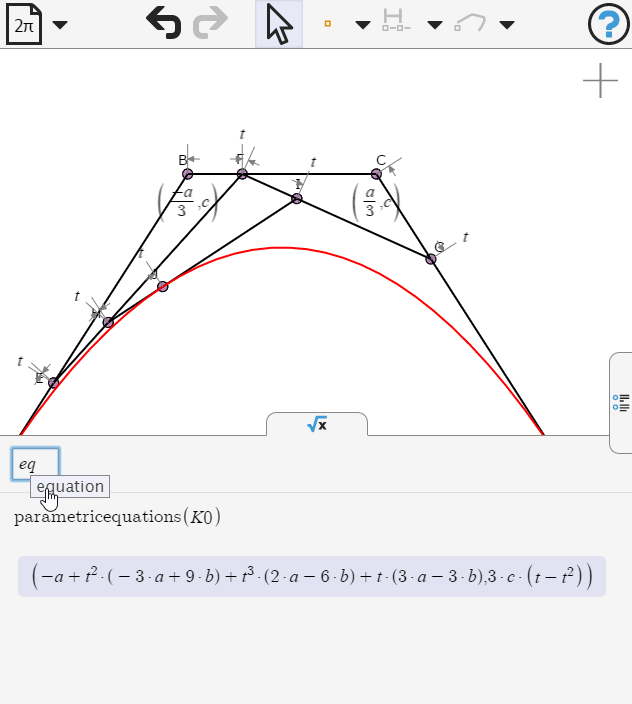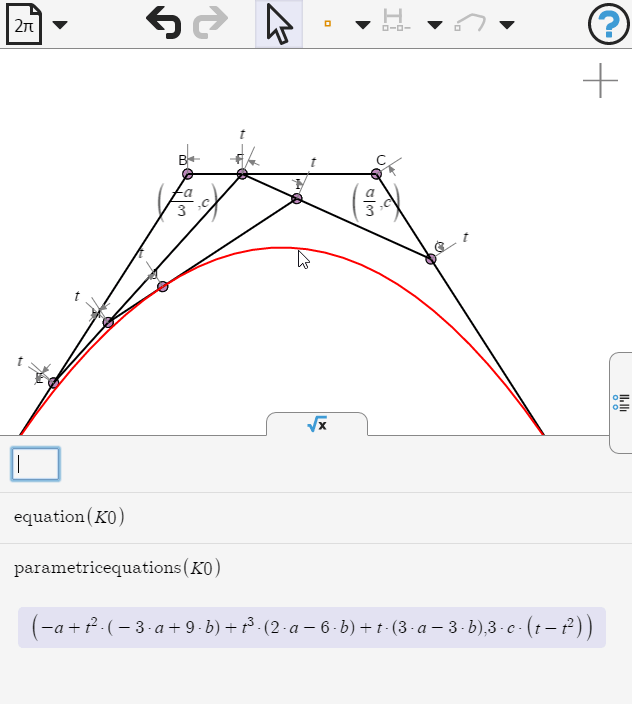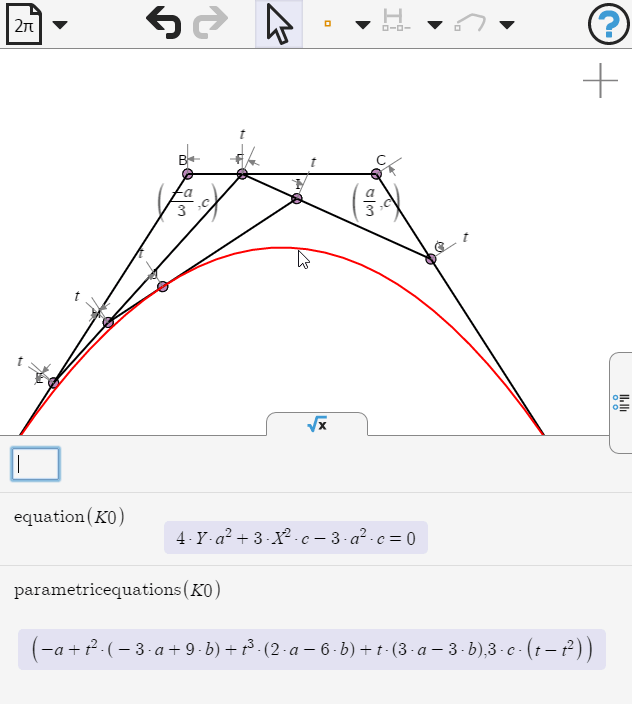
We edit the coordinates of point B and C, replacing b by a/3

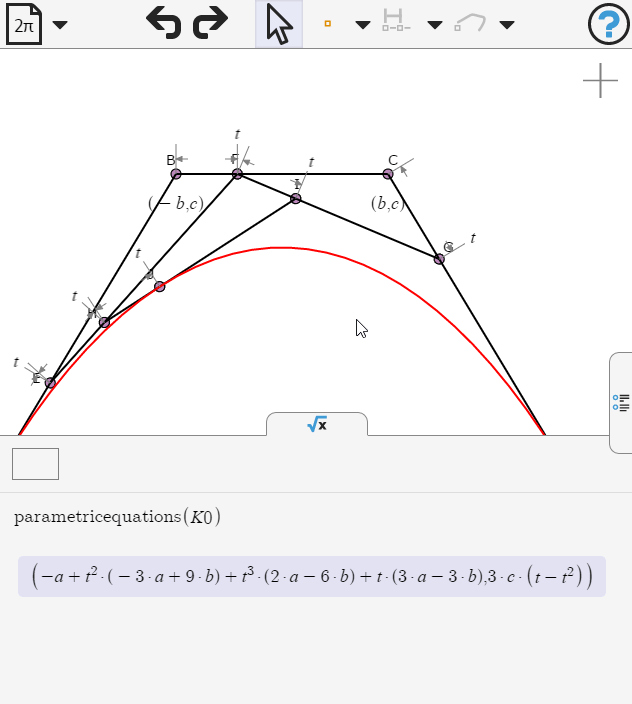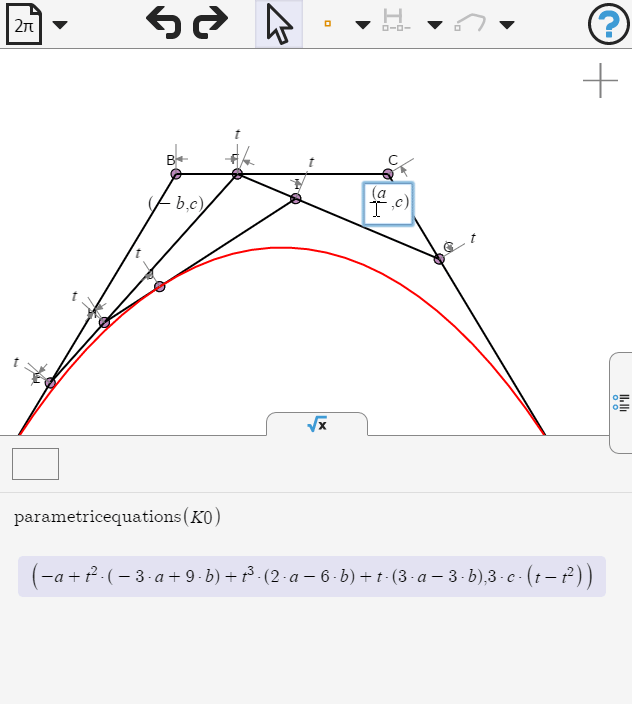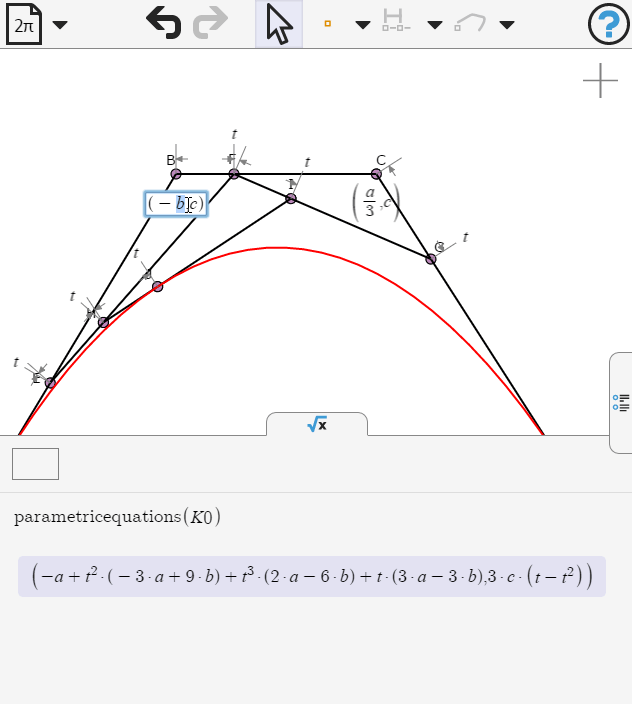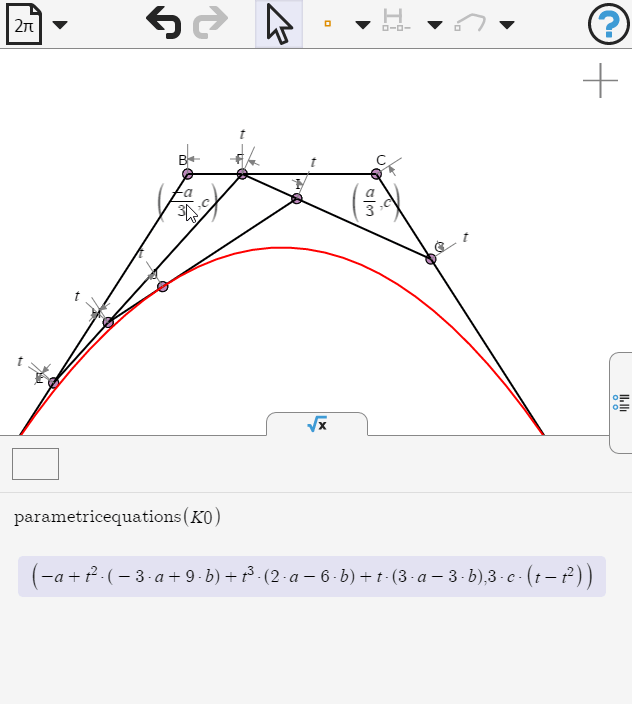
Now we can examine the equation of the curve. What kind of curve is this?