Solar Cooker
A simple solar cooker consists of a box with a reflective lid.
If the box is positioned horizontally, and the sun is at angle φ to the horizontal, what angle should the lid be opened to?

A simple solar cooker consists of a box with a reflective lid.
If the box is positioned horizontally, and the sun is at angle φ to the horizontal, what angle should the lid be opened to?
We first create a pair of line segments representing the top of the box and the lid.
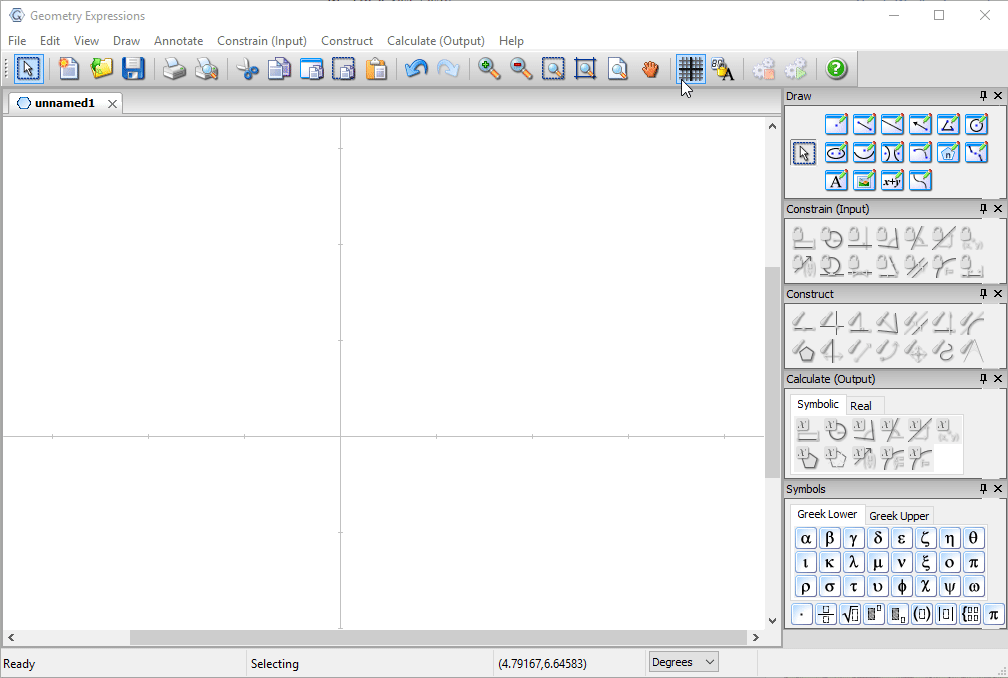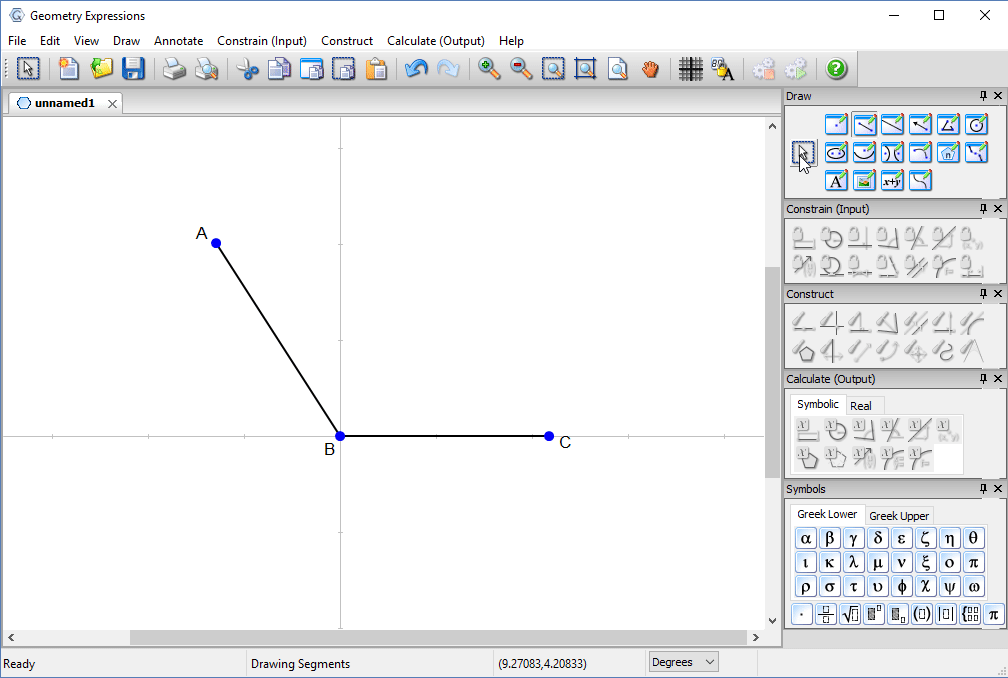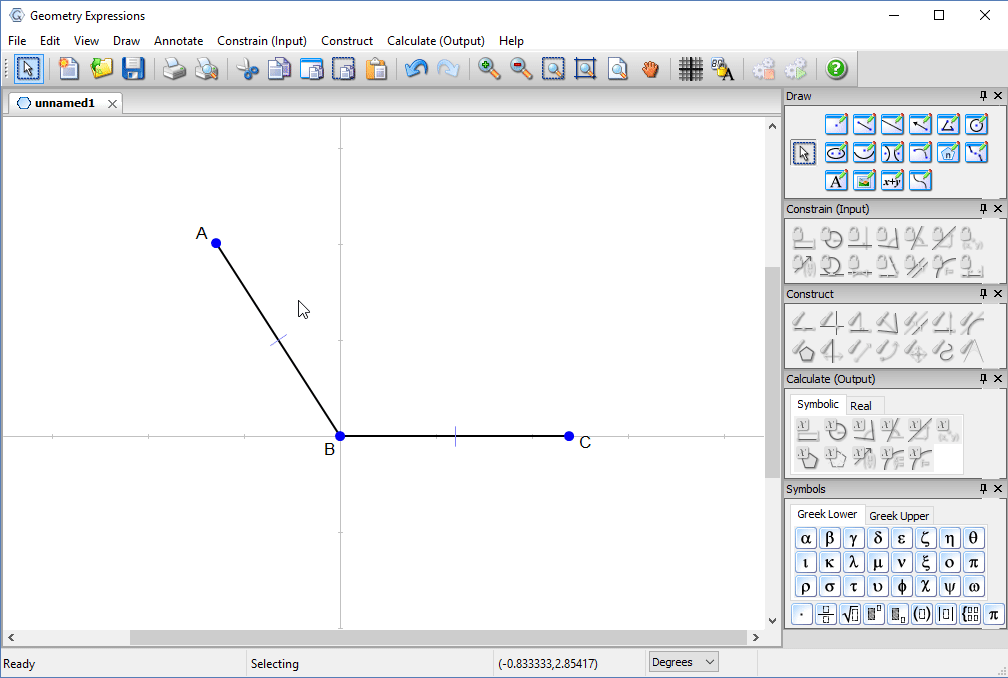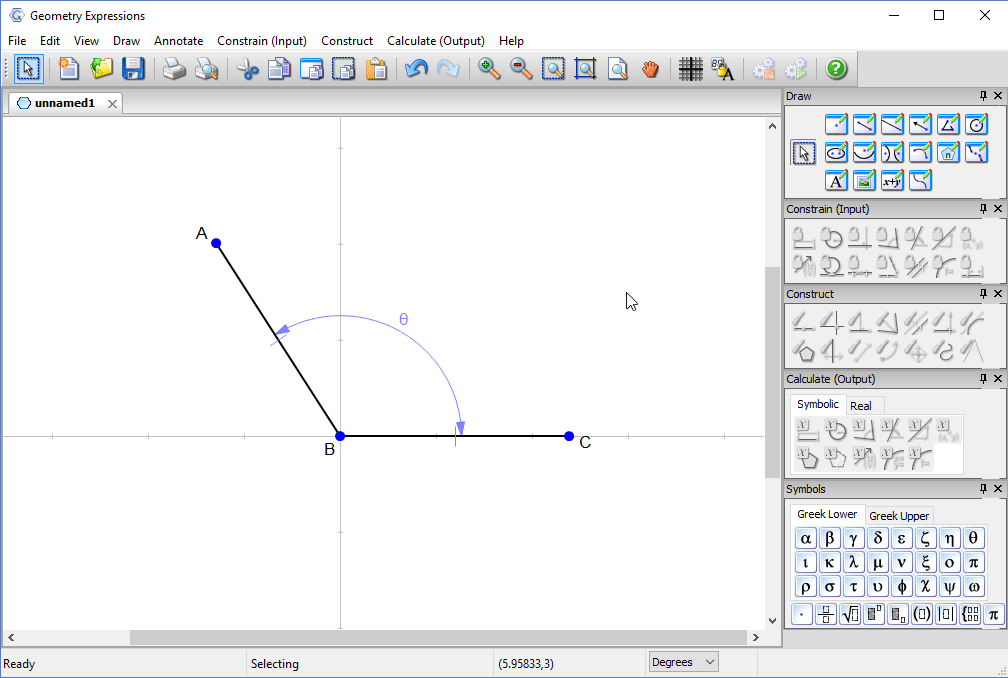
We constrain them to be congruent and constrain the angle between them to be θ.
We now create a line (representing a sunbeam) through the edge of the box, and reflect it in the box.
We constrain the sunbeam to be angle φ to the horizontal .
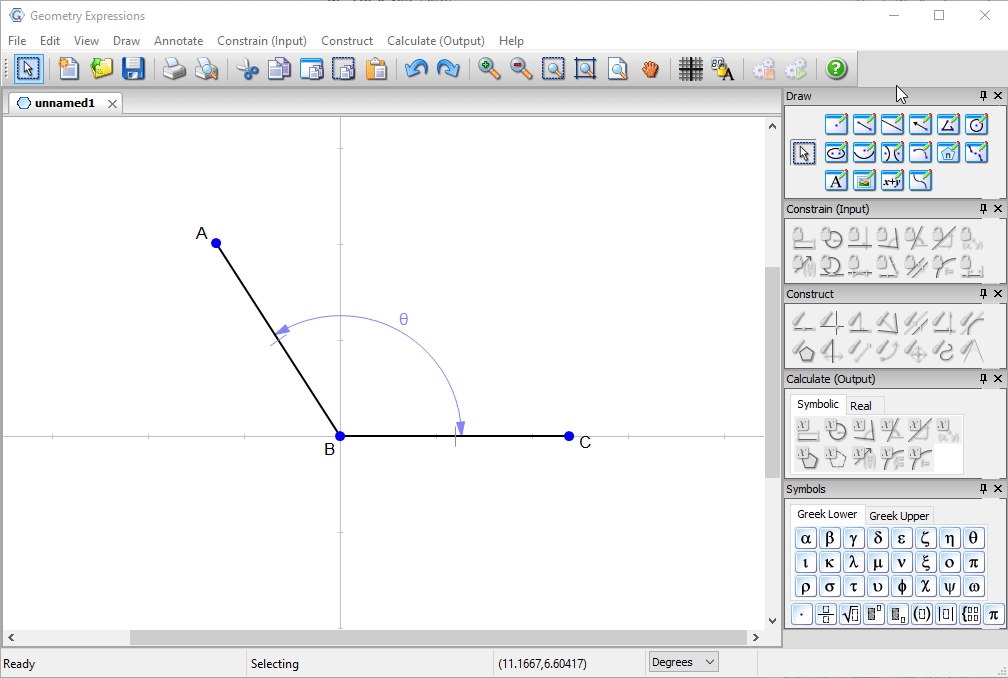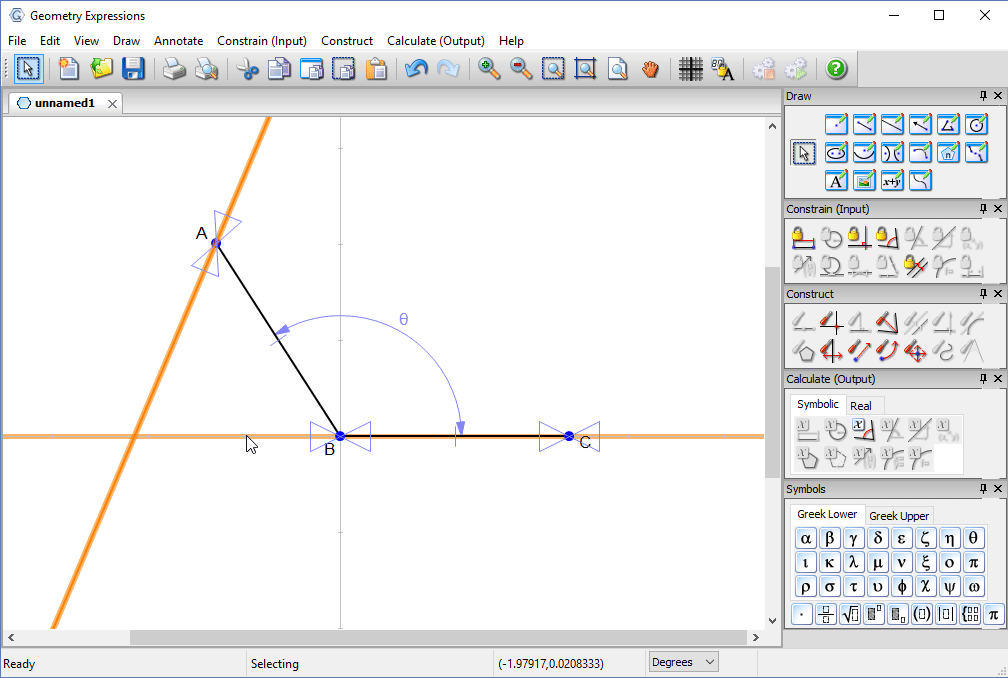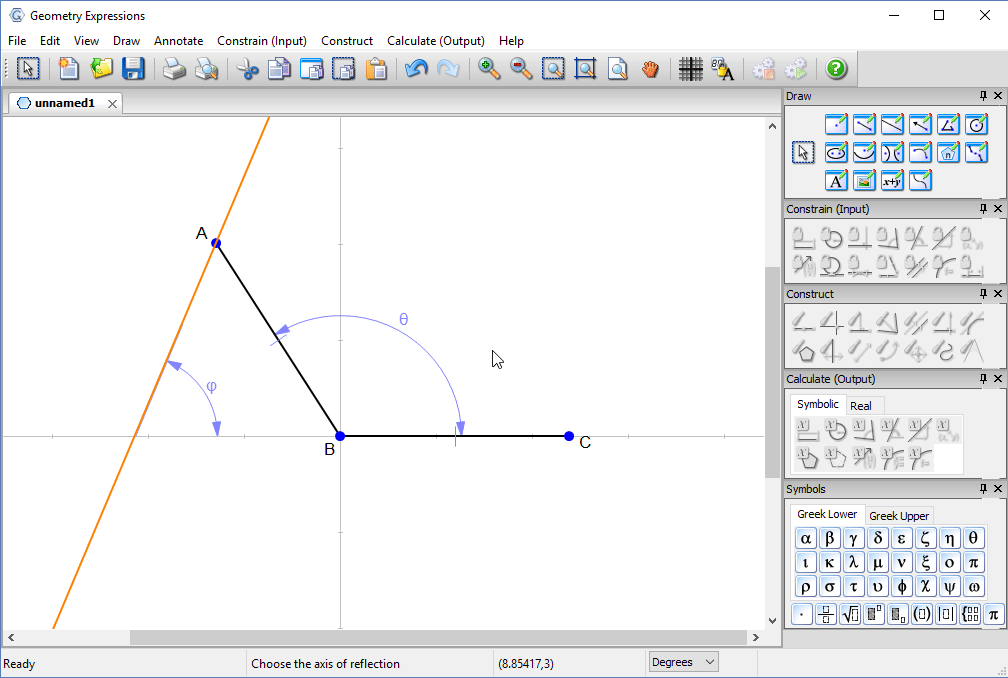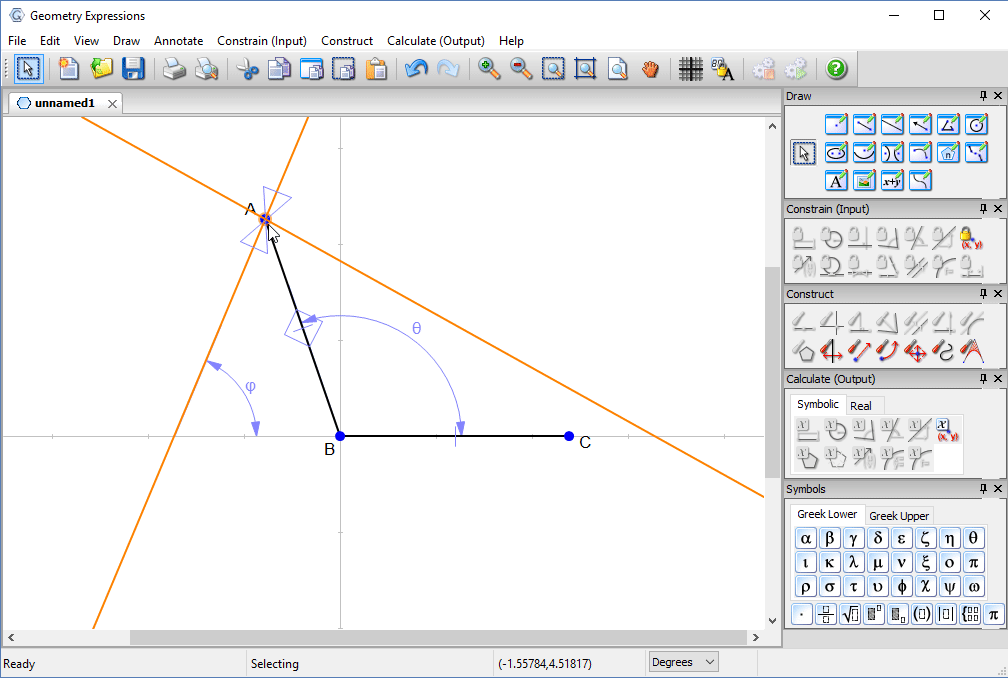
We examine the angles made by the reflected ray with the lid and with the horizontal.
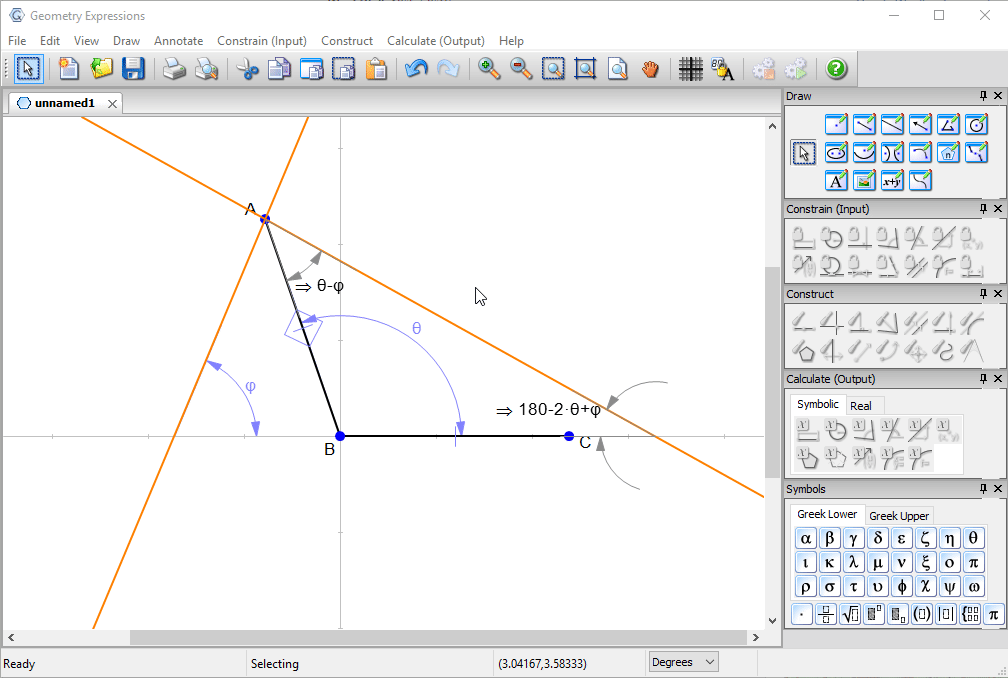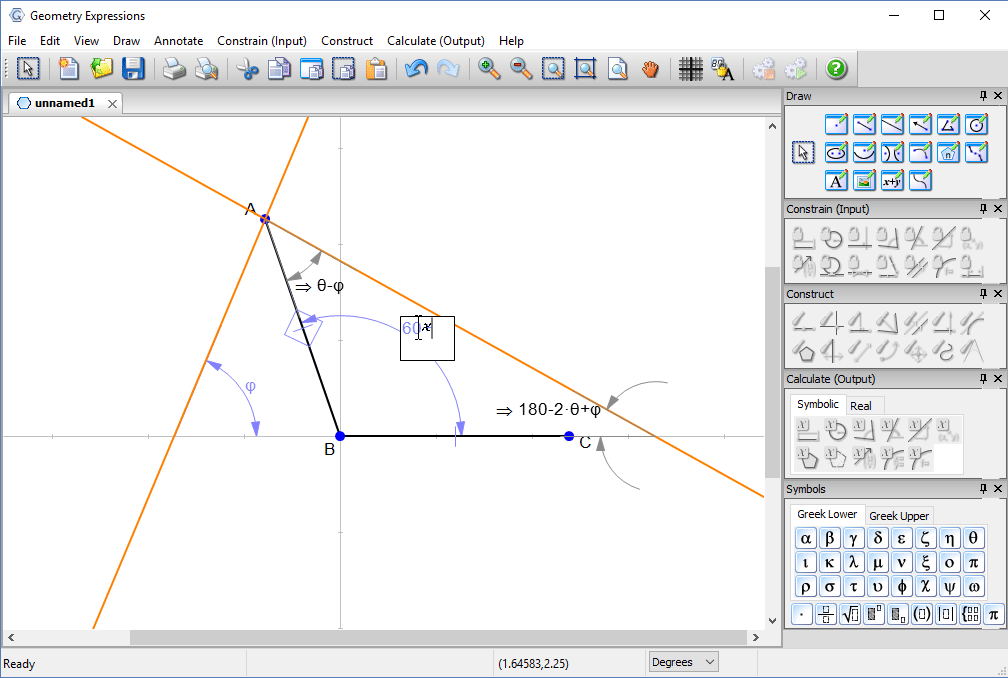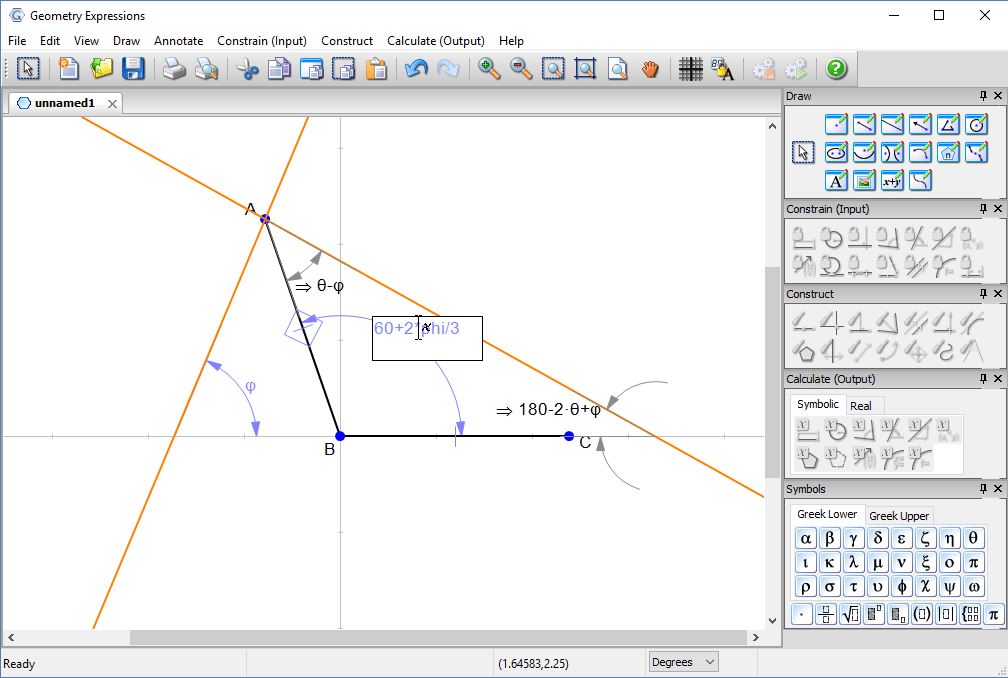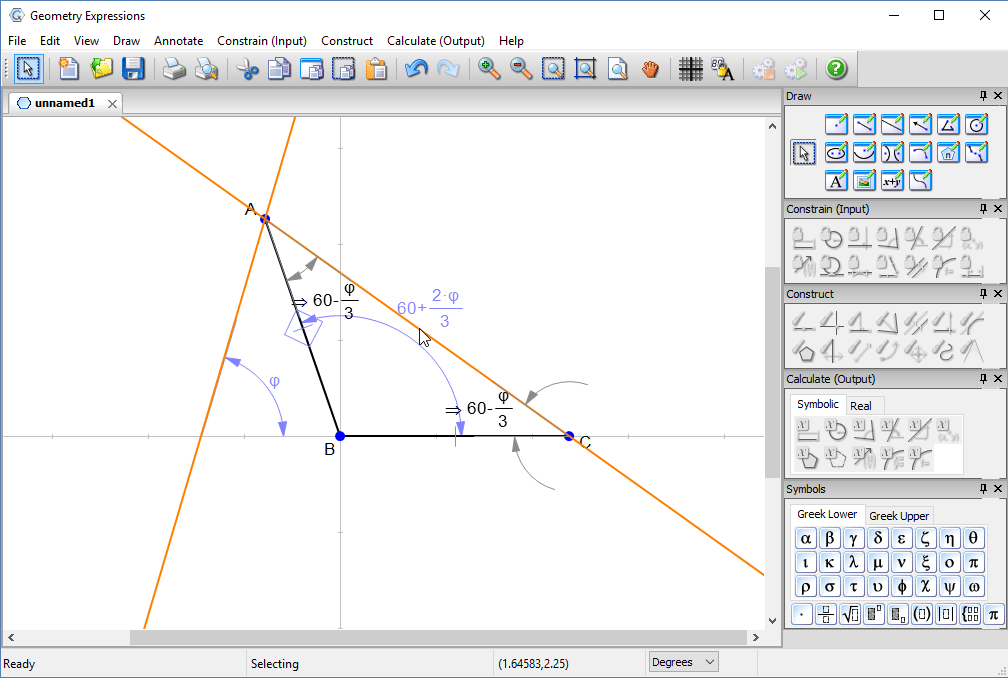
With a little thought, we can convince ourselves that the best angle for the lid will be when the reflected ray touches the edge of the box.
That is, when the two angles are equal.
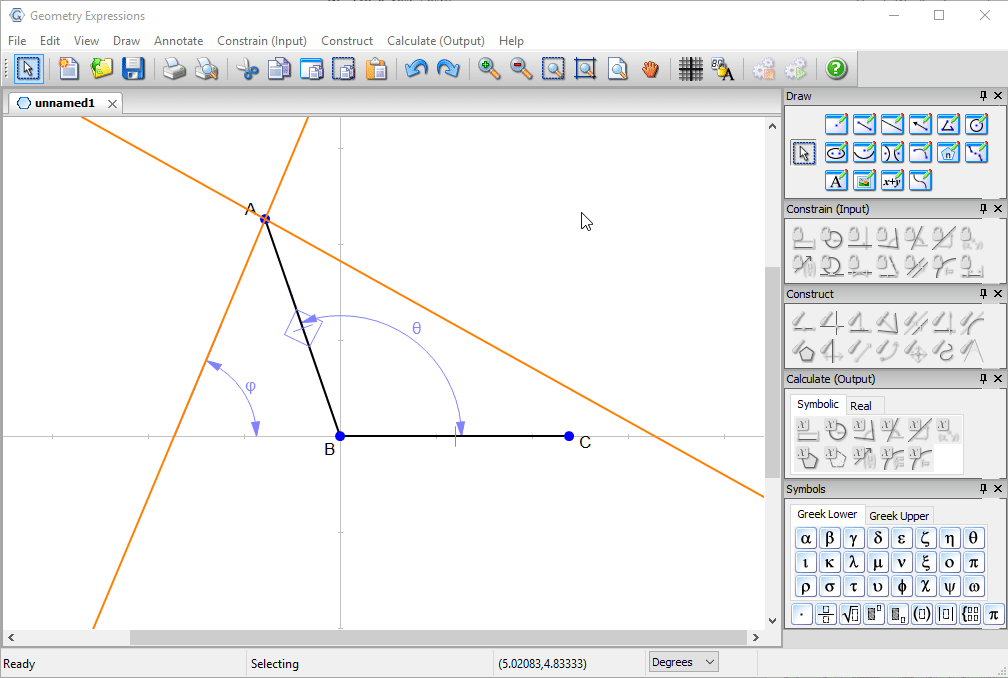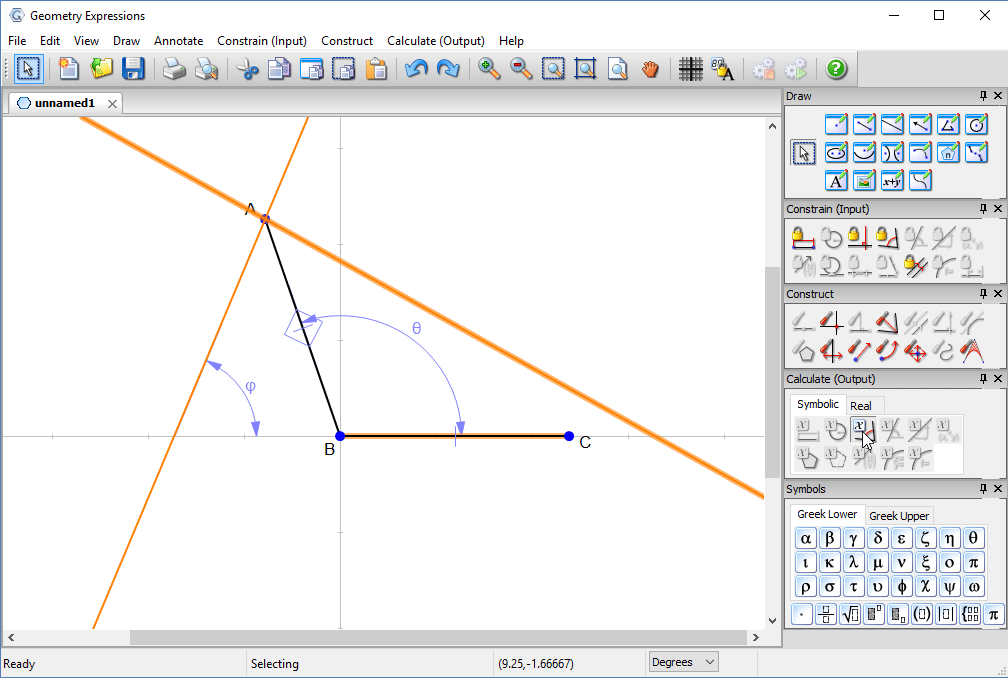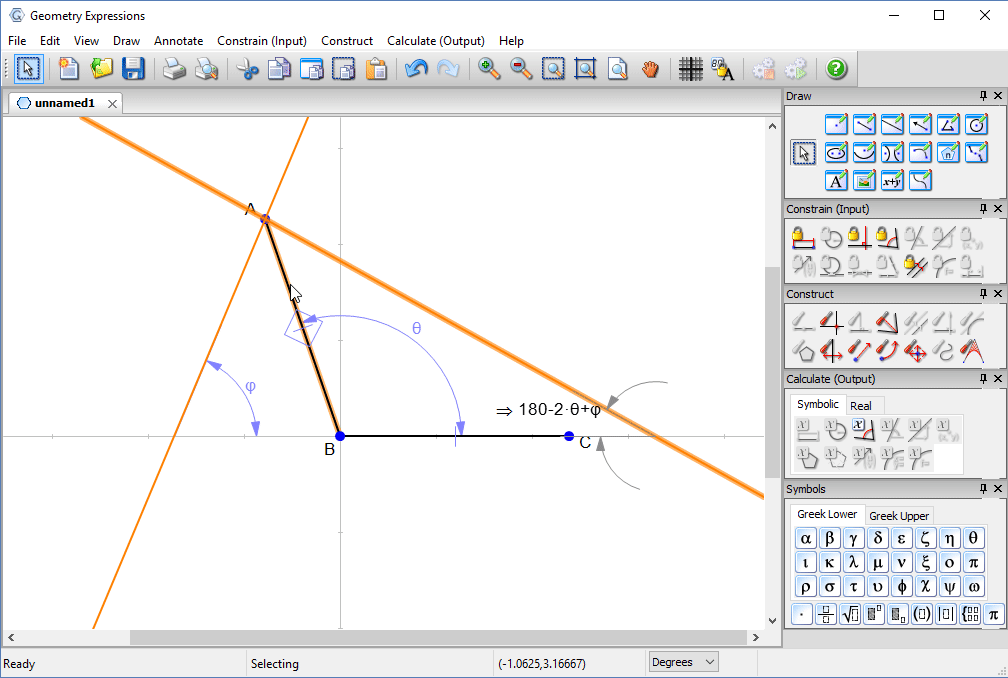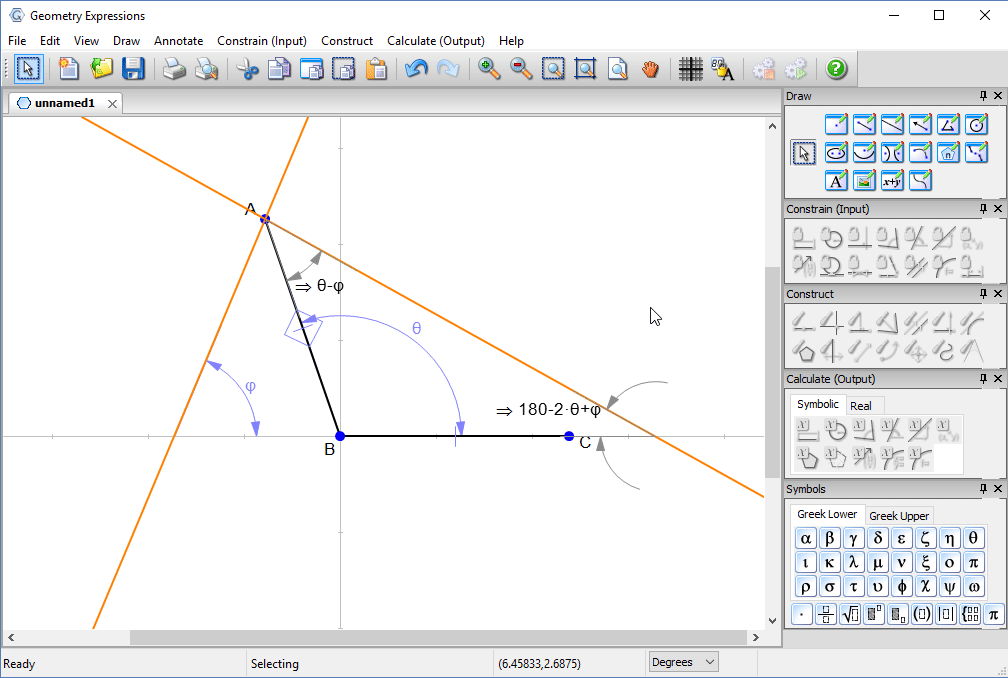
You can solve for θ by hand, and type in the answer to see the solution.