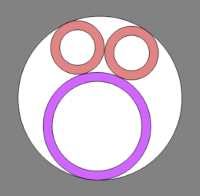
Pipes
Three pipes of different radii need to fit through a circular hole.
What is the radius of the smallest hole they'll fit through?

Three pipes of different radii need to fit through a circular hole.
What is the radius of the smallest hole they'll fit through?
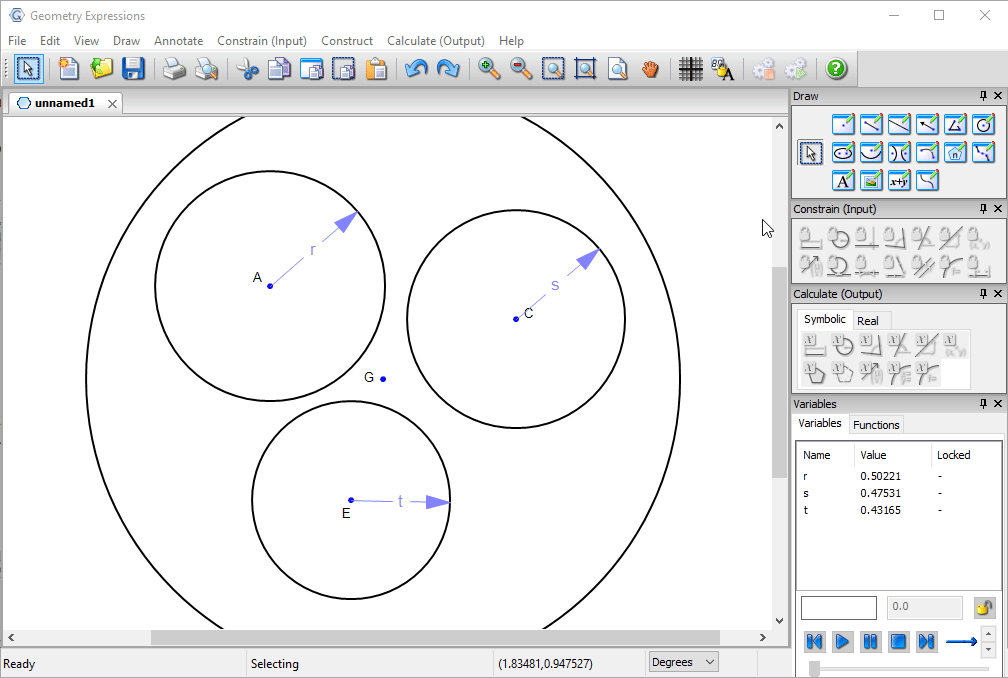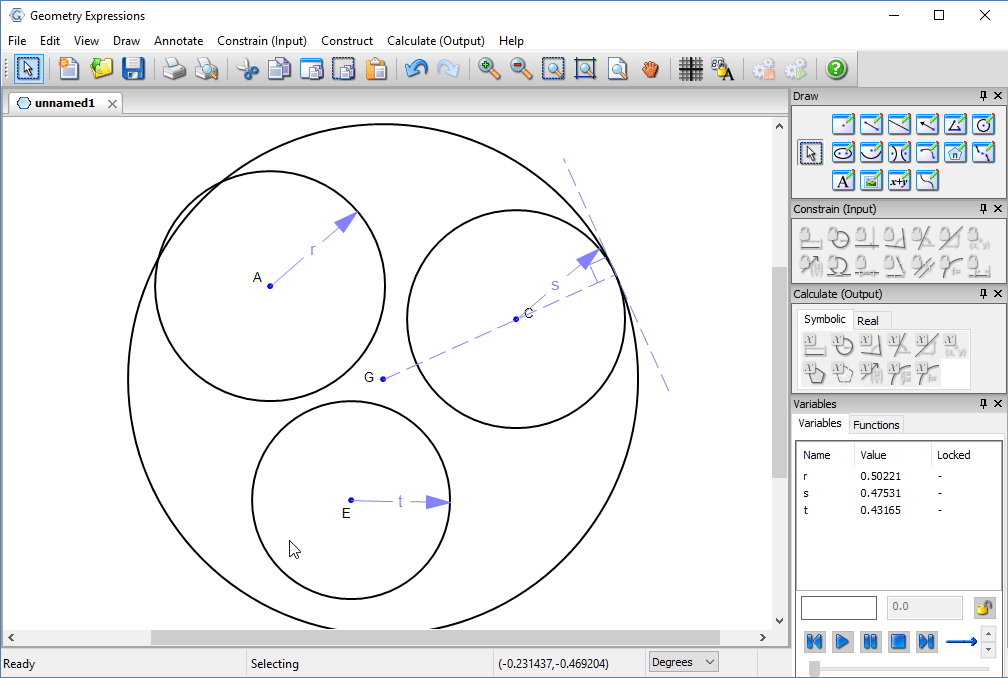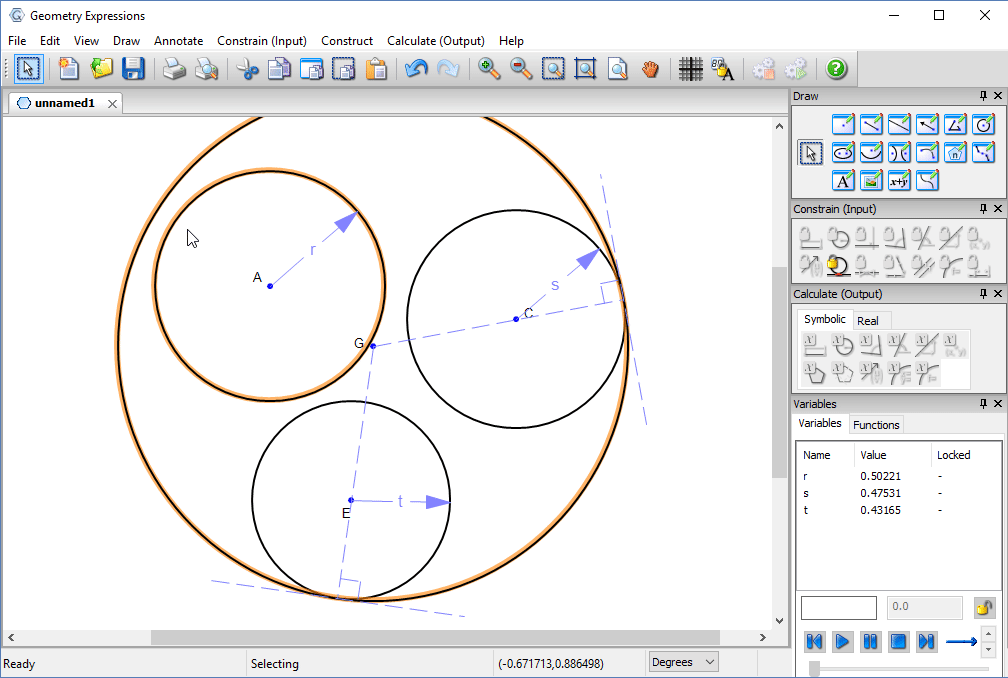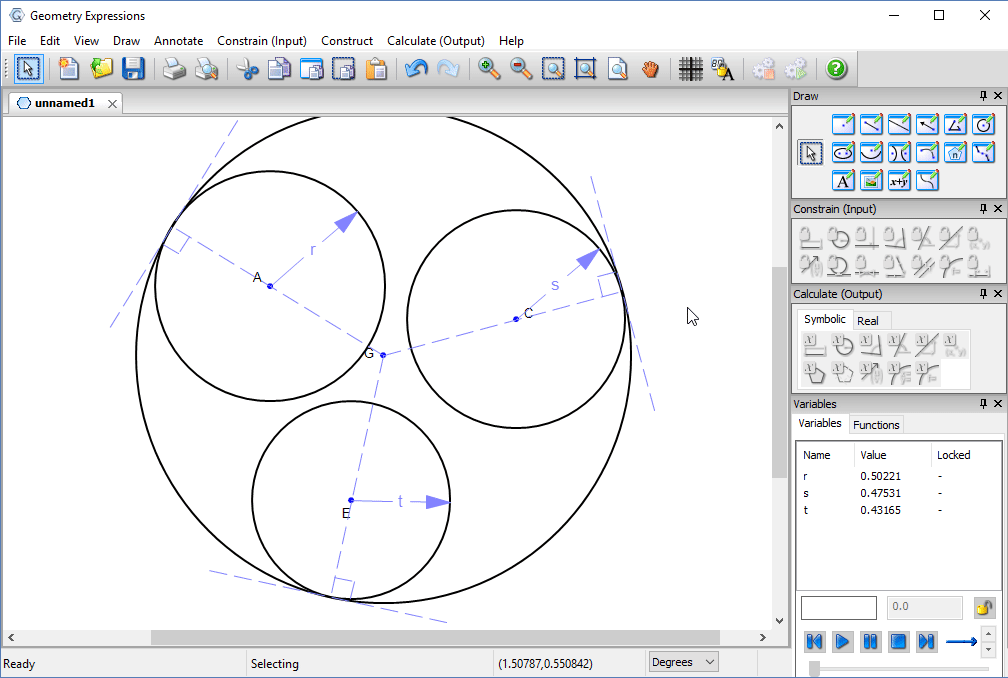
First we draw circles representing the pipes, and specify their radii.
We draw a hole which is big enough.

We can make our hole smaller, by constraining it to be tangent to the three pipes.
We can make it even smaller by constraining the pipes themselves to be tangent.
The radius of the outer circle, in terms of the pipe radii would seem to answer our problem.
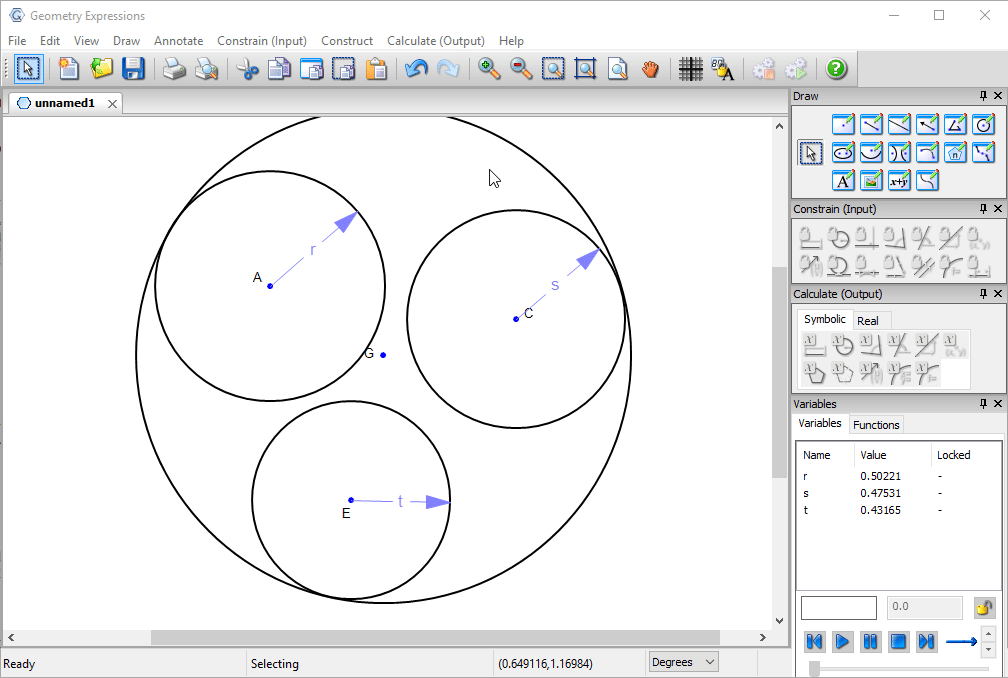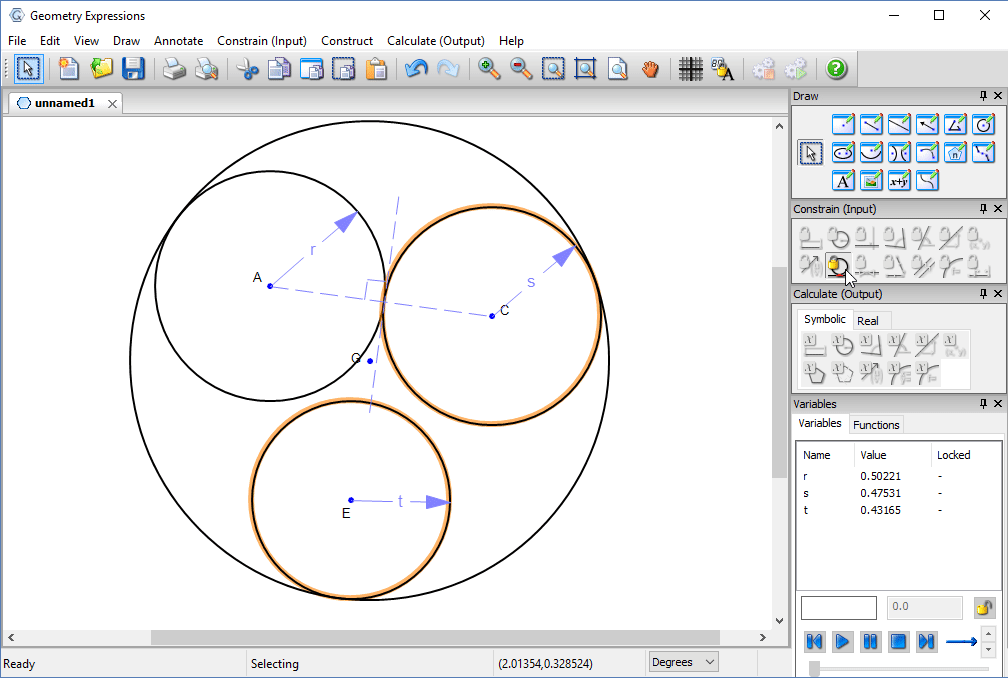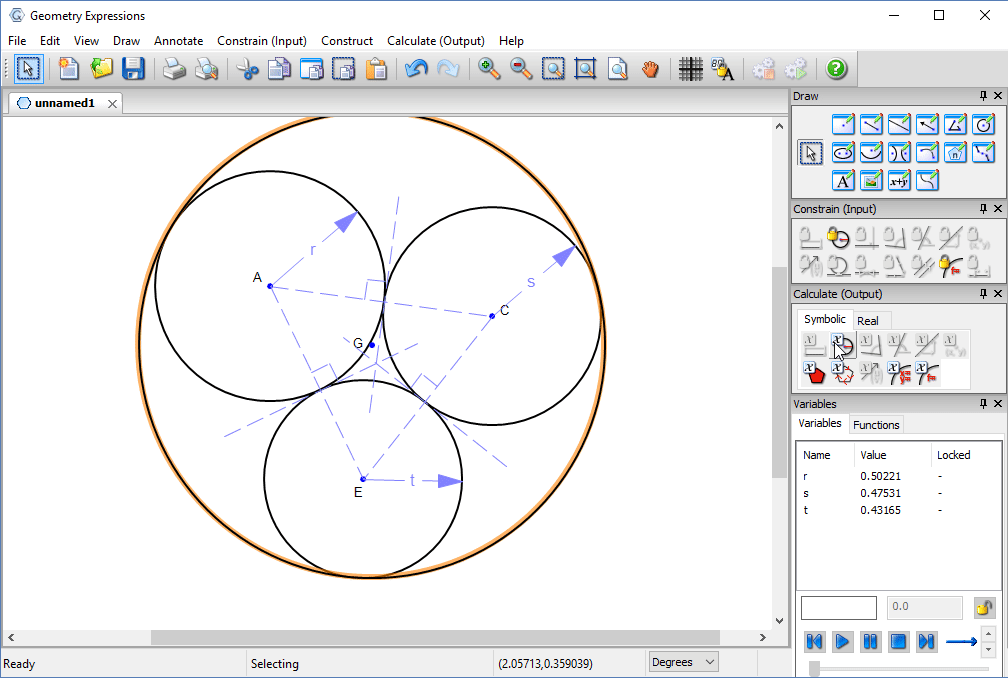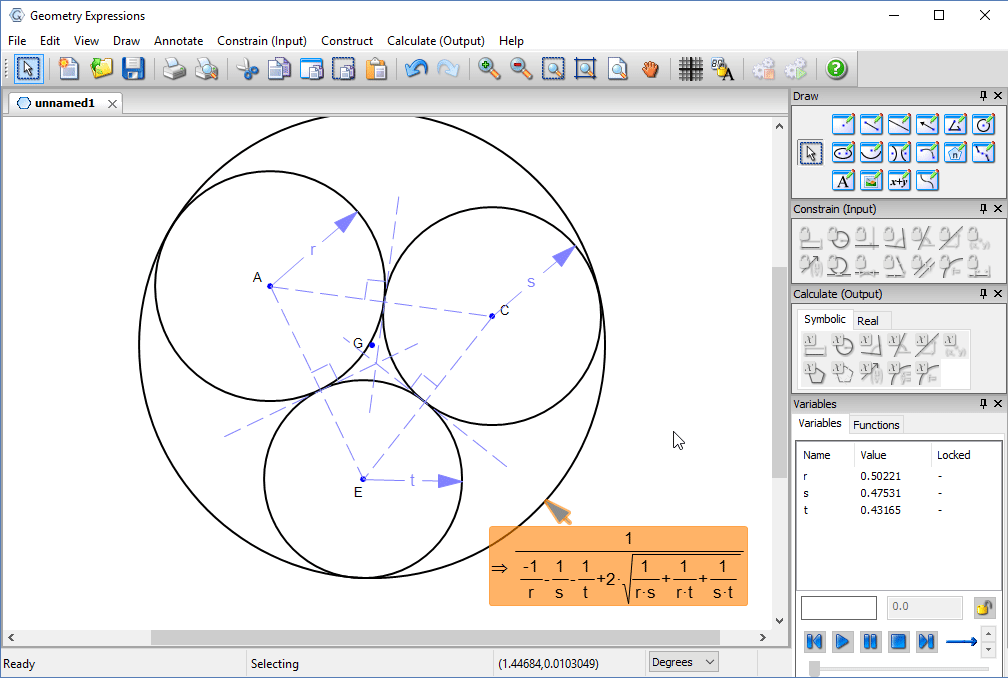
However, if we vary t the radius of one of the pipes, we see that as it gets smaller, the hole we have defined gets larger and larger.
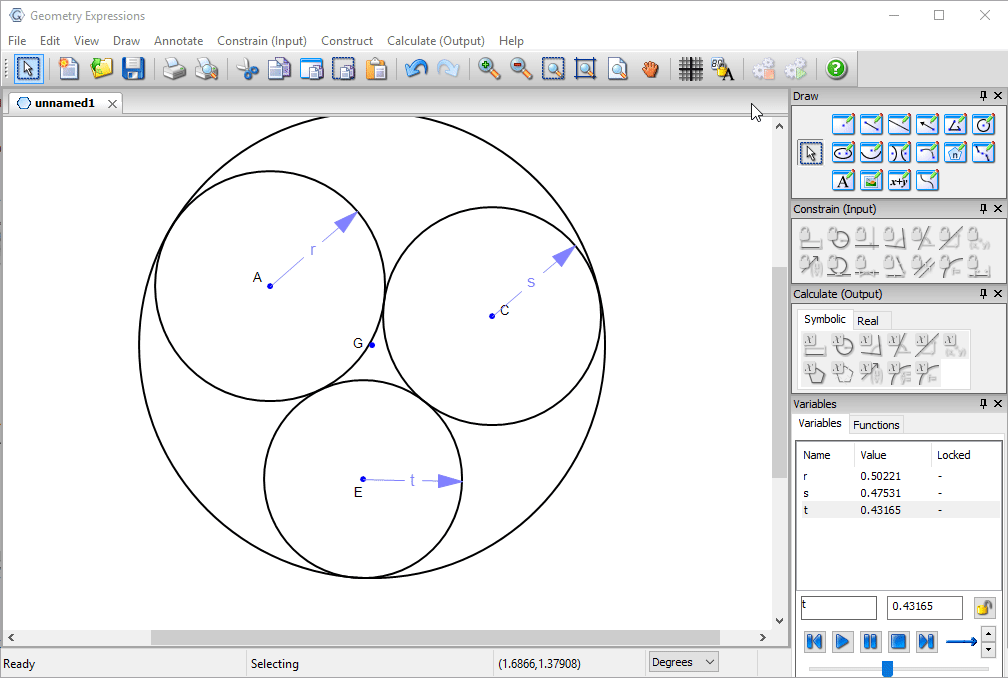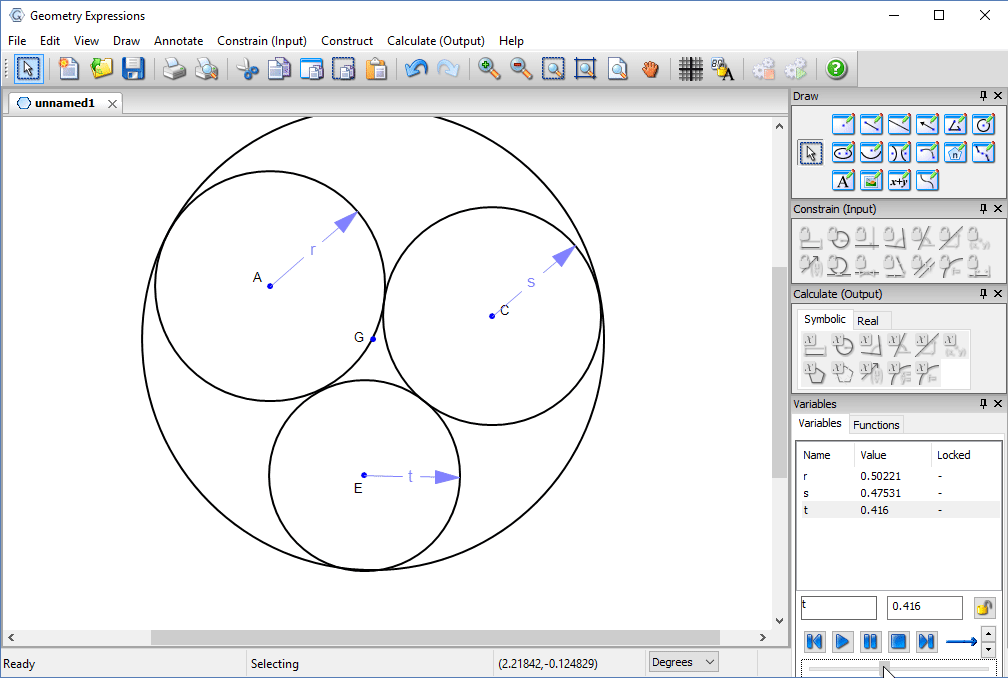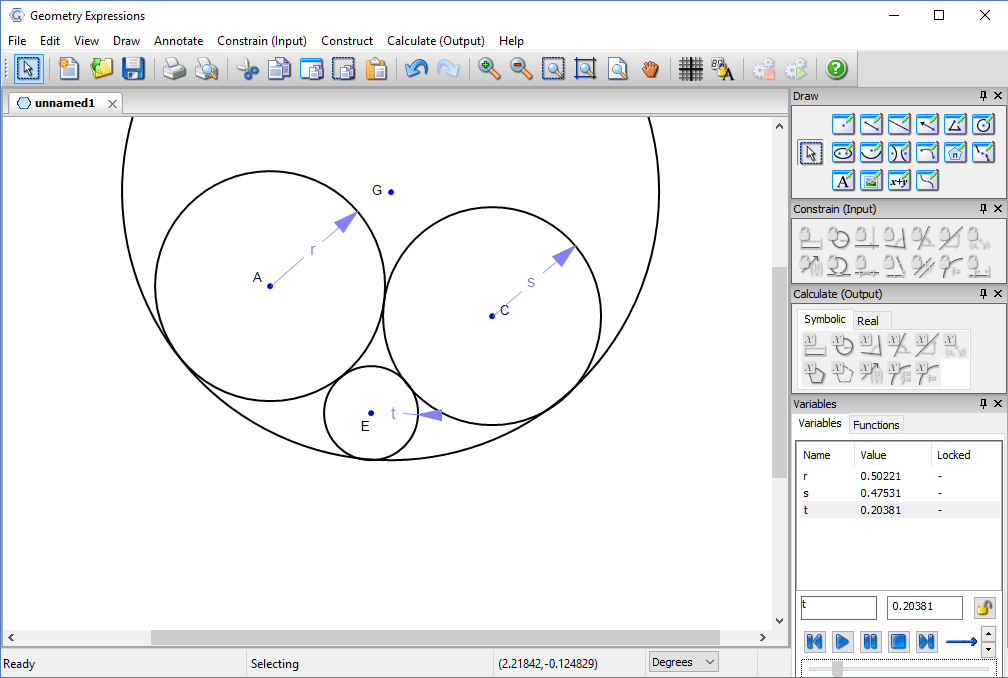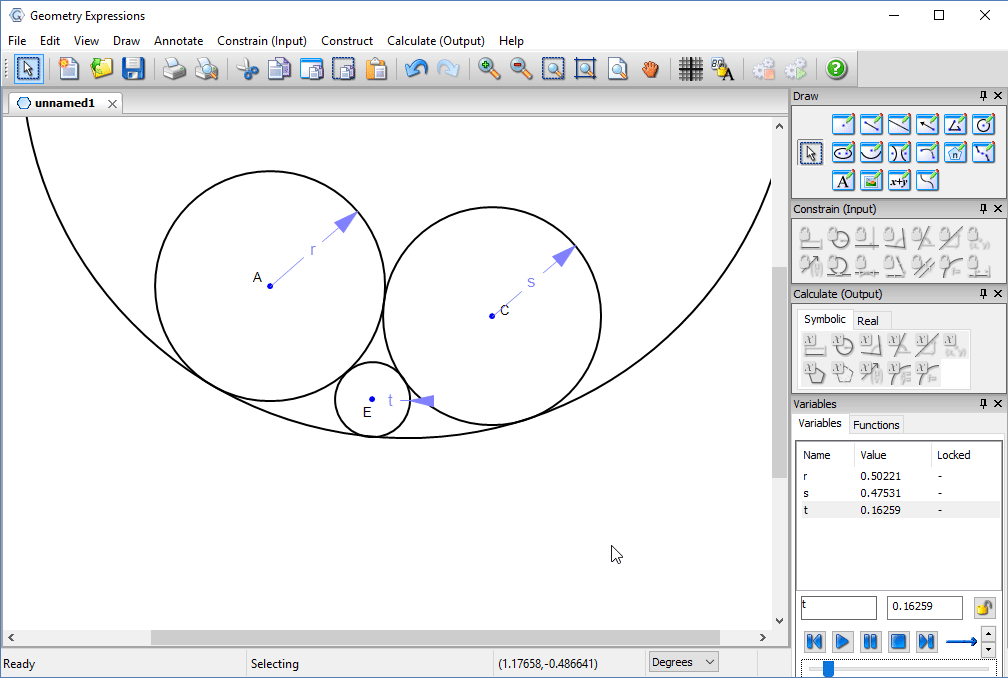
In fact it is possible to make a much smaller hole: the hole tangent to the two larger circles whose radius is equal to the sum of their radii.
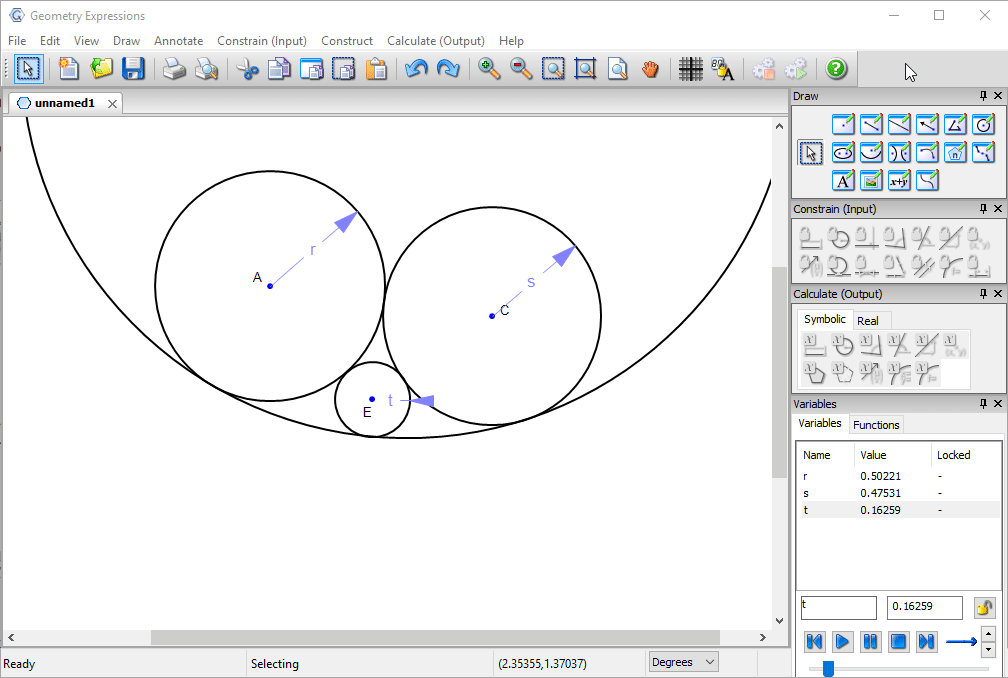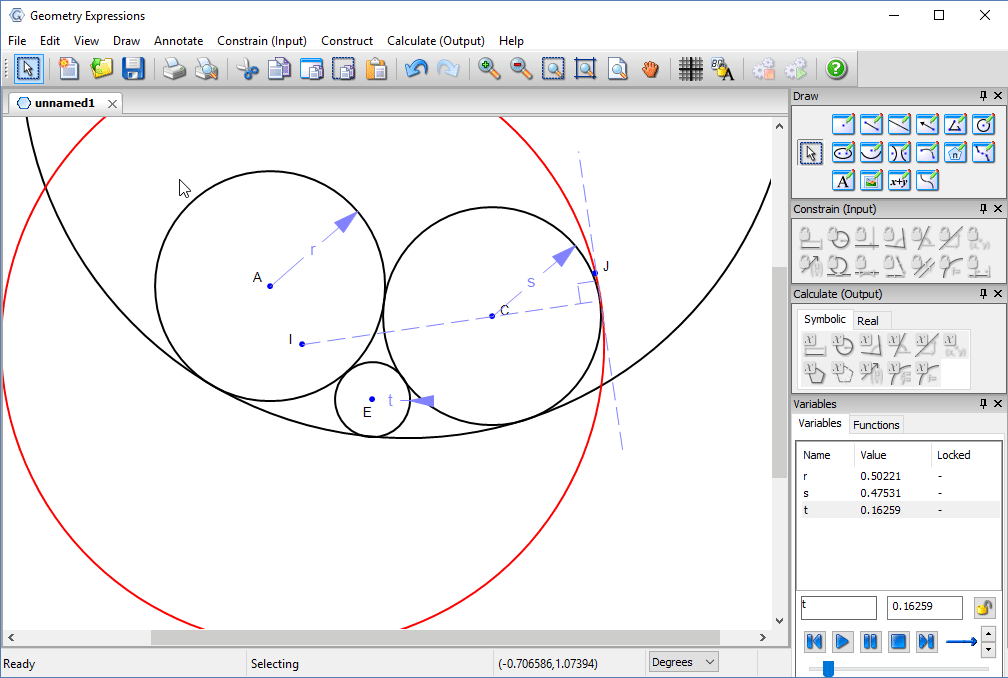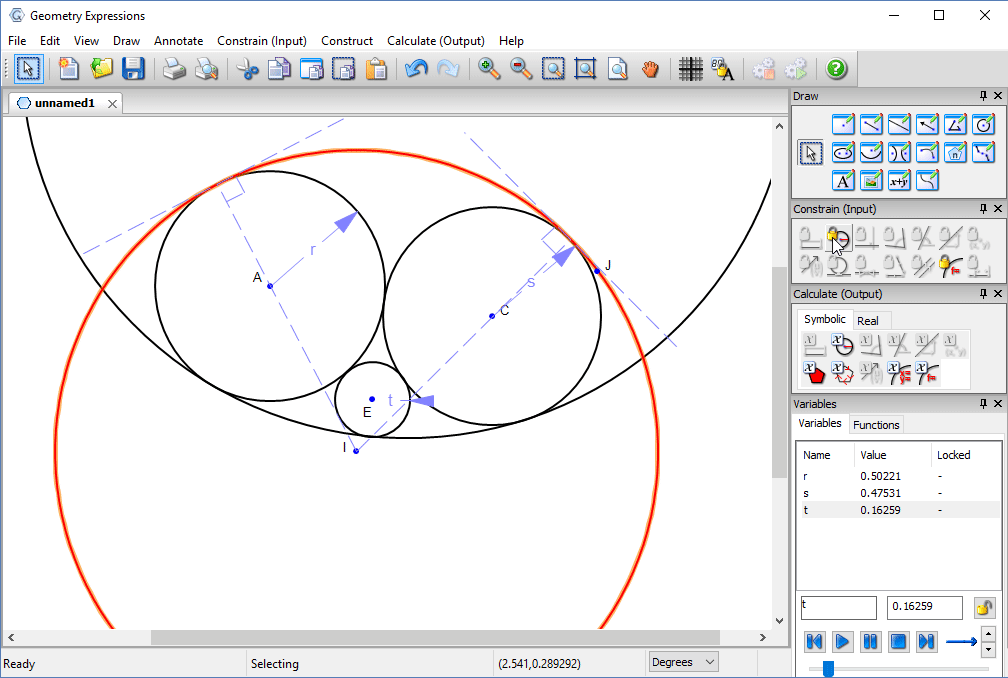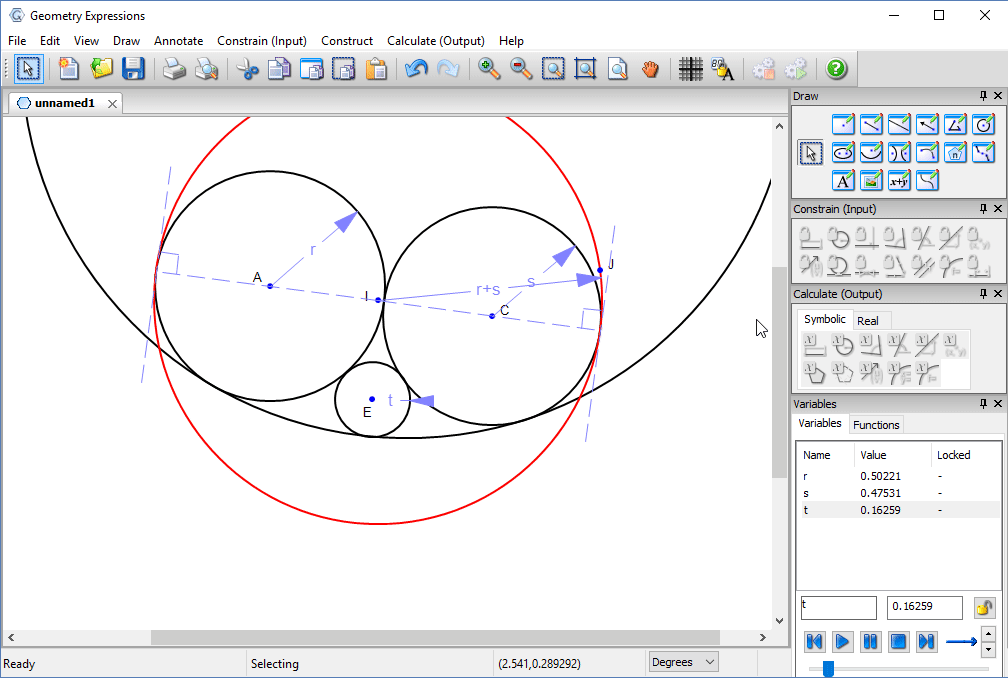
Under what conditions does this solution pertain?
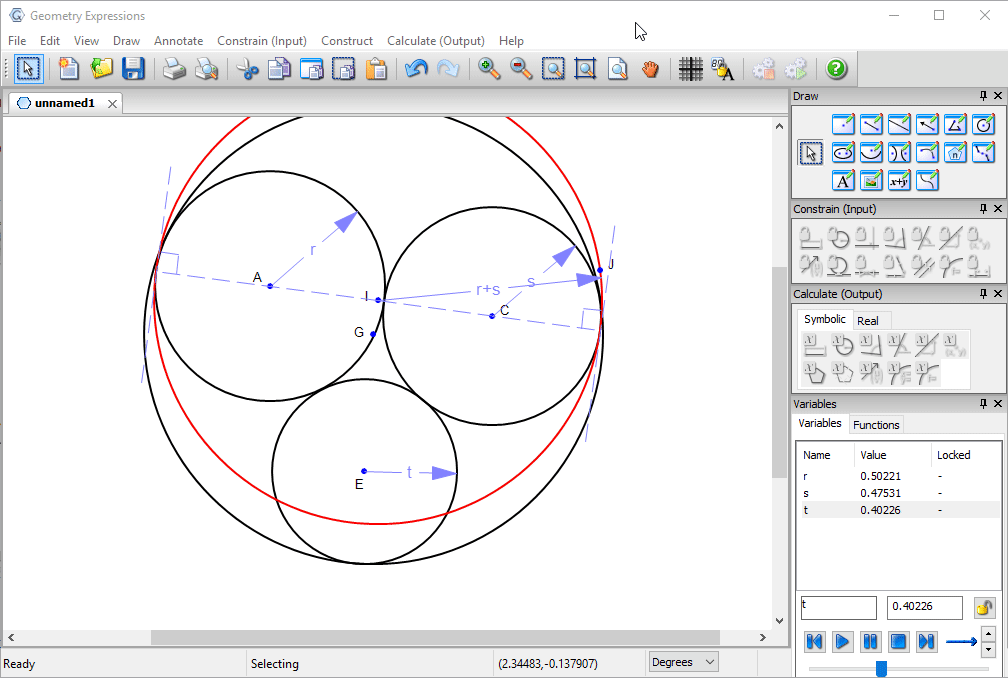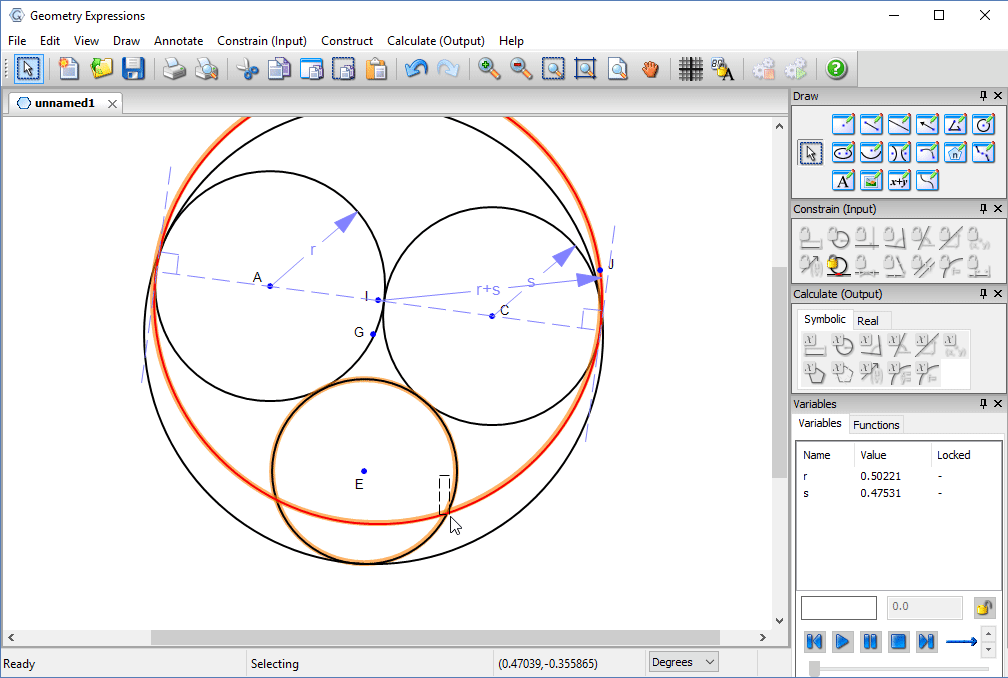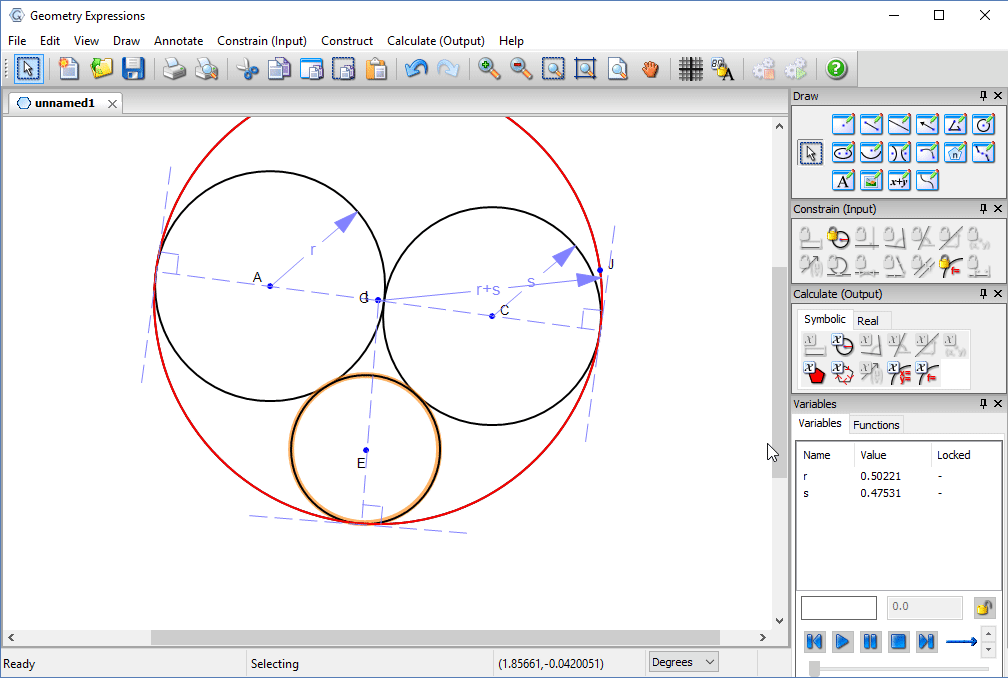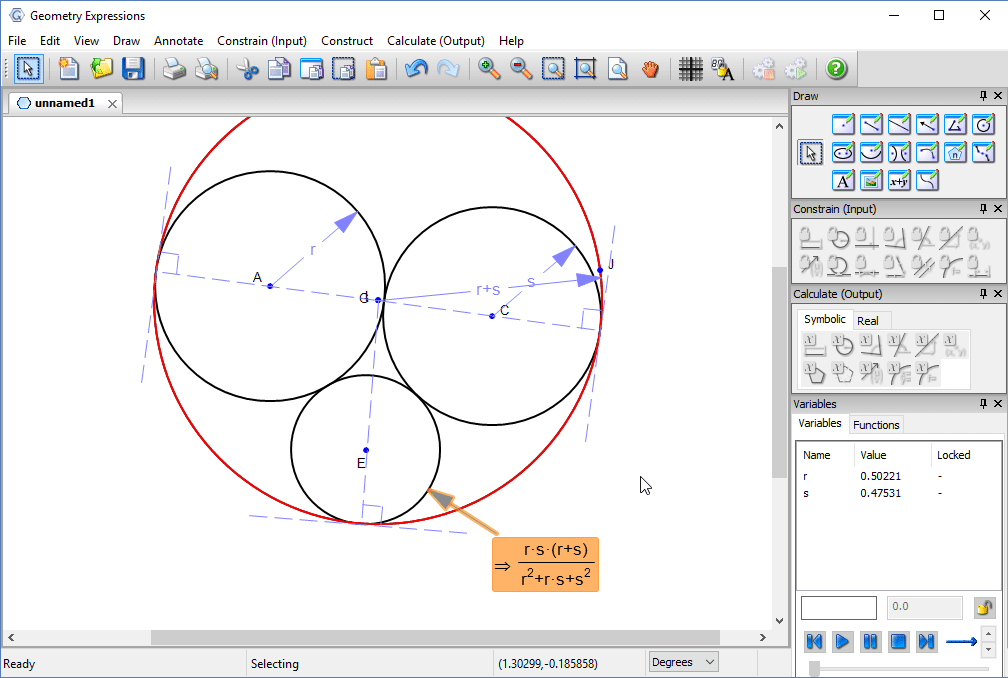
Some experimentation will convince us that the critical value for t is where the circle centered at E is tangent to the red circle is tangent to the red circle.
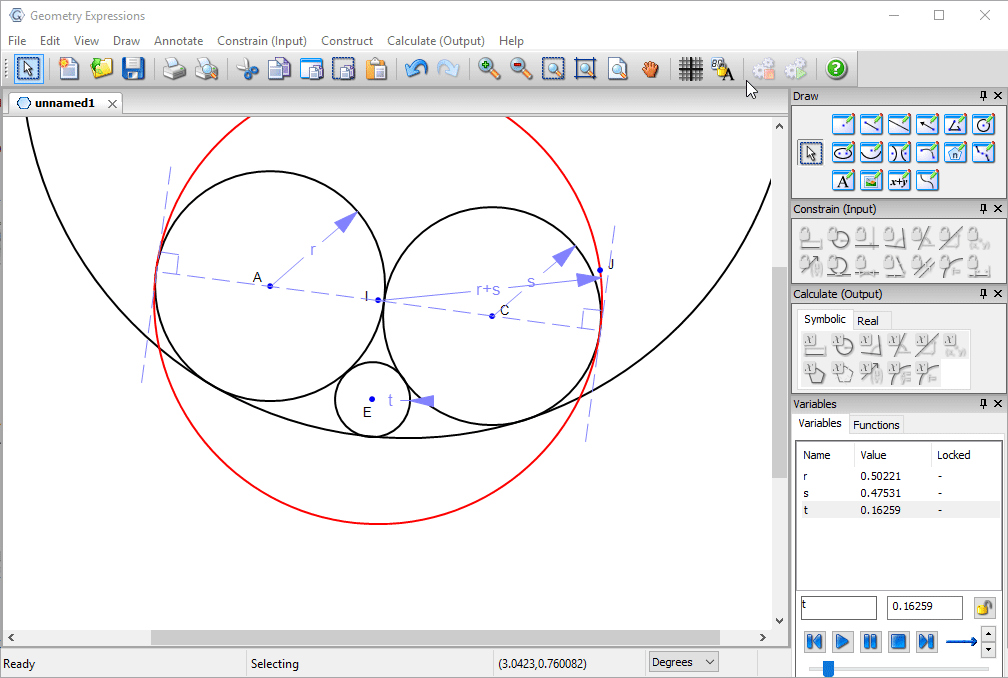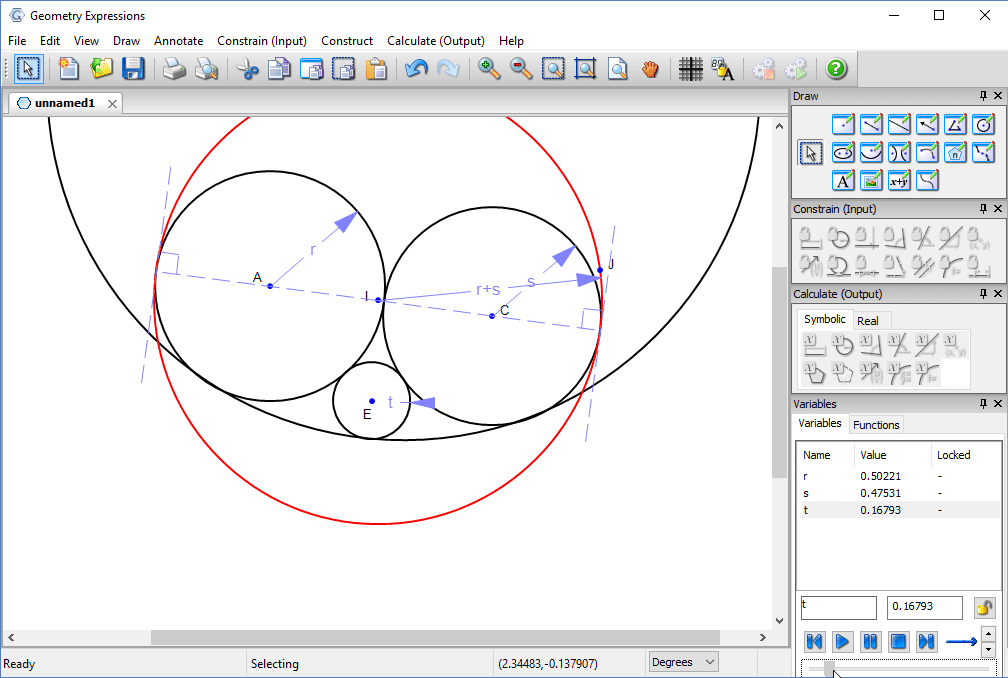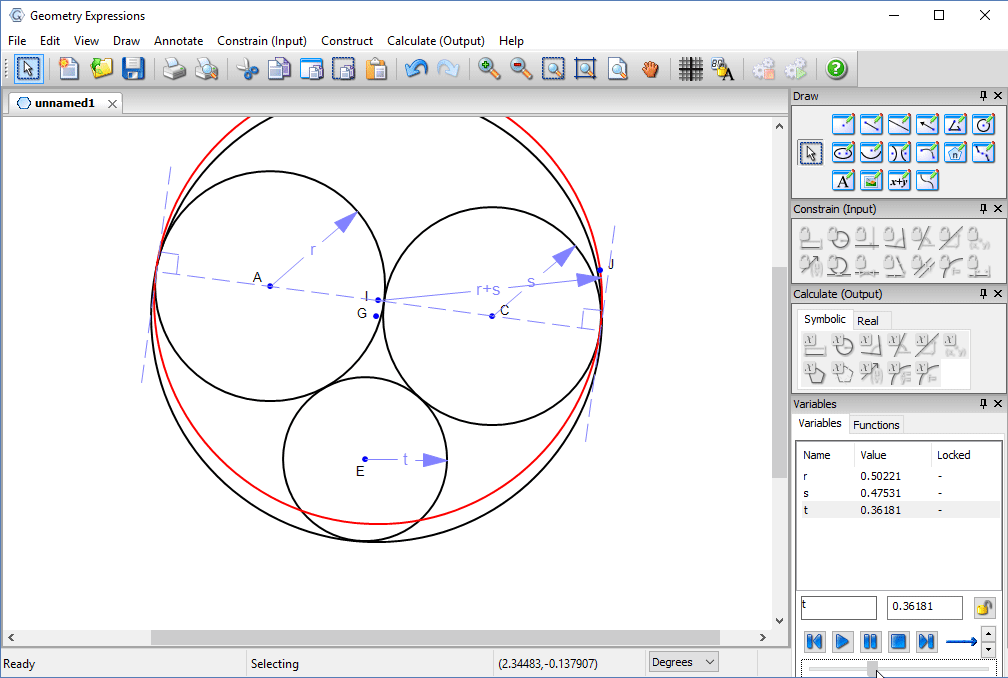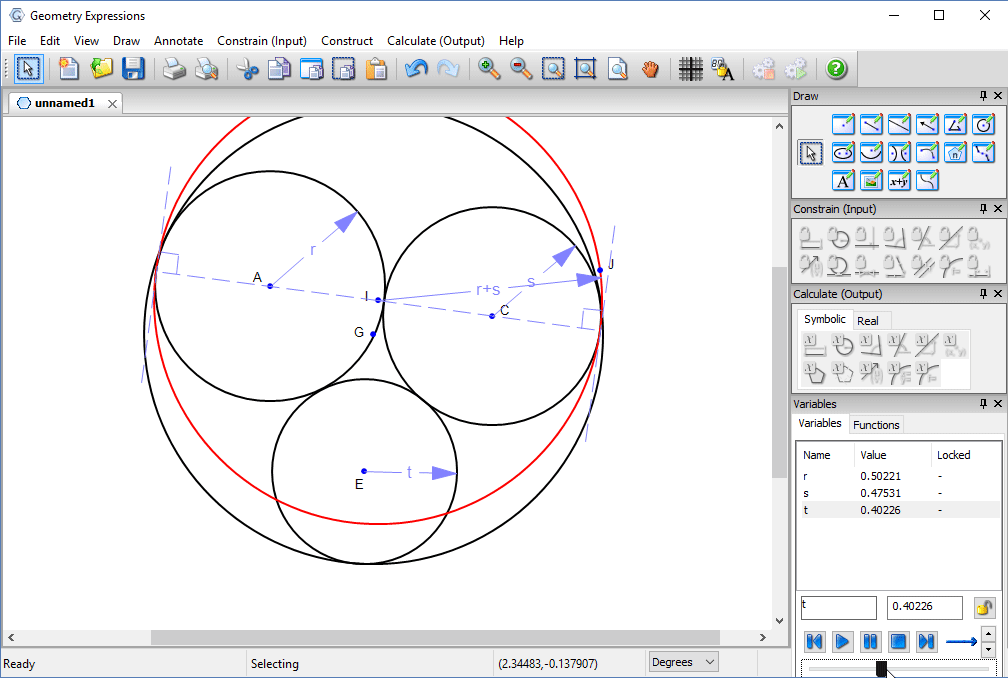
This value can be found by removing the radius constraint and adding a tangency constraint, then measuring the radius.