Best Solar Concentration

A simple solar cooker consists of a box with a reflective lid.
We ask the question: What is the most sunlight a box like this can capture, and what angle would the lid be at this best case?

A simple solar cooker consists of a box with a reflective lid.
We ask the question: What is the most sunlight a box like this can capture, and what angle would the lid be at this best case?
We start with a pair of congruent line segments modeling the box and the lid.
We assume that in the best configuration, incoming light touching the edge of lid will be reflected over the edge of the box.
This is modeled by drawing a line between A and C and reflecting it in AB.
A parallel line through C completes the drawing.
We wish to find a configuration which maximizes the distance between the parallel rays.

We specify the length of the box to be 1. We could constrain angle ABC, but instead, we constrain the distance AC to be x
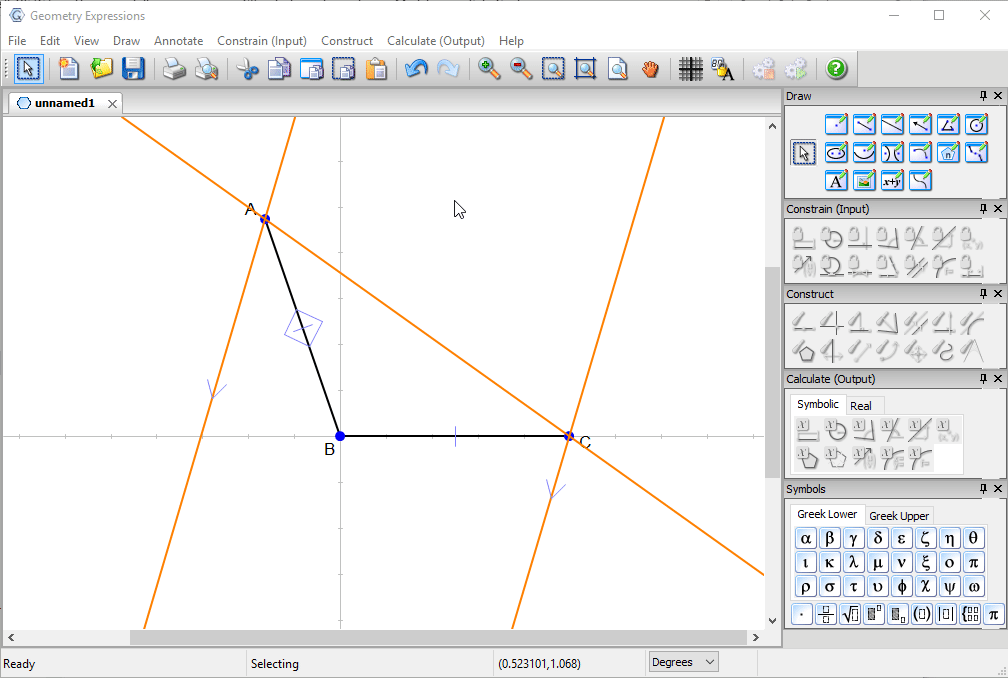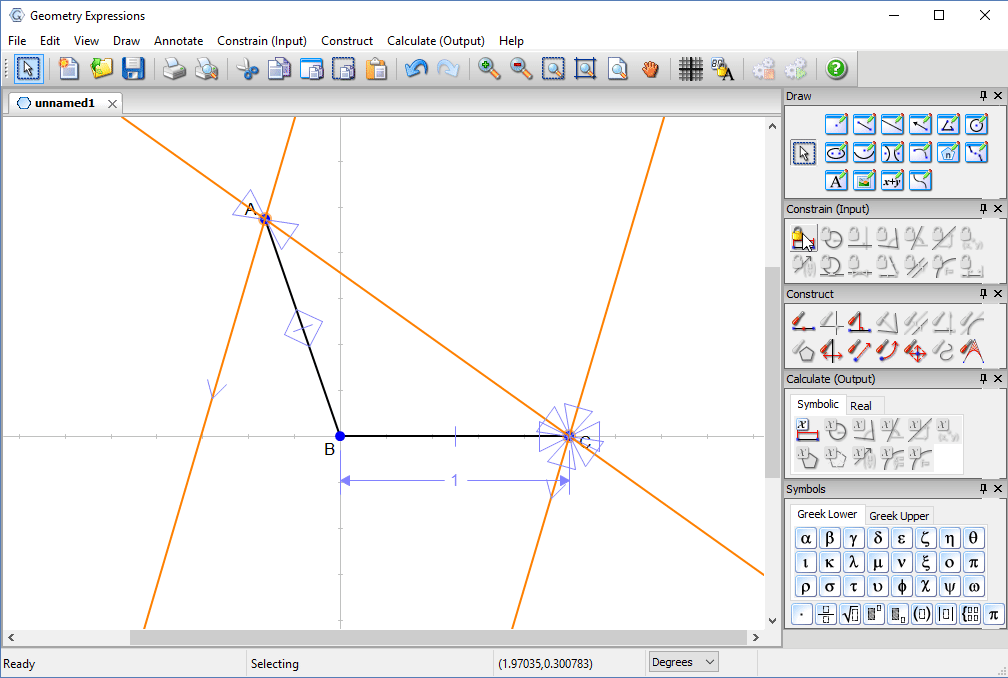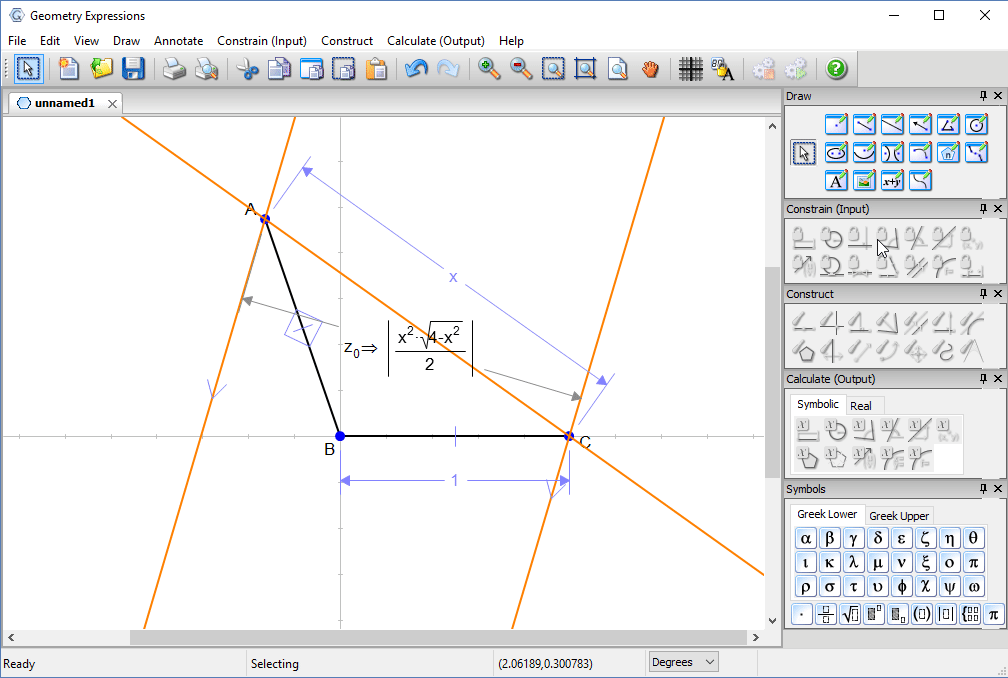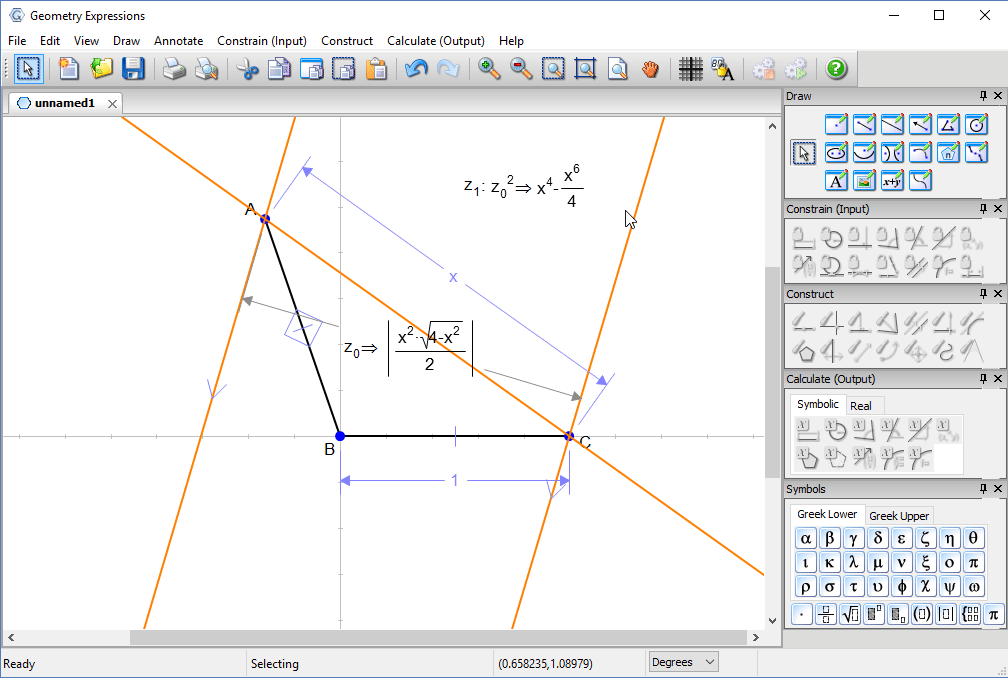
We can now ask for the distance between C and the reflected ray. This is the distance between the two rays.
We would like to find a maximum for this value, which contains a square root. Squaring it gives a simpler expression, whose maximum will be found at the same value of x.
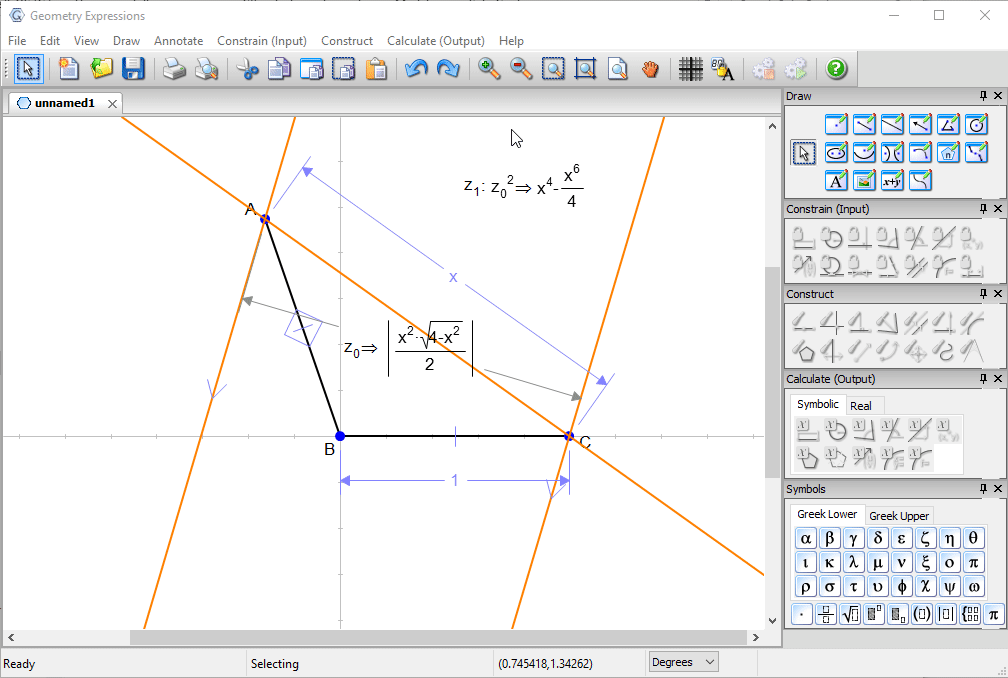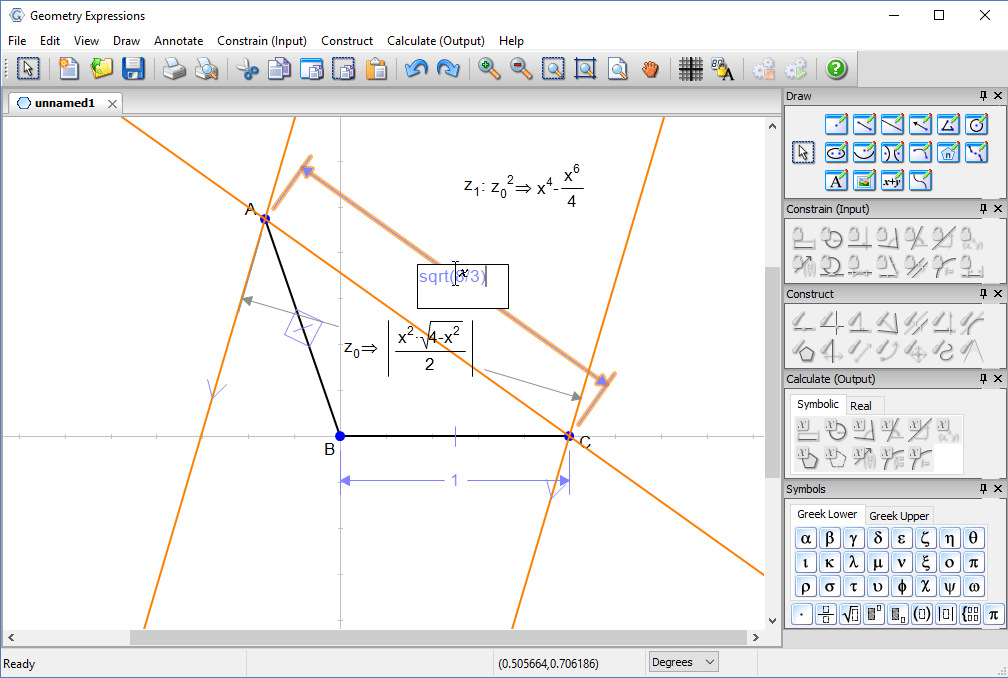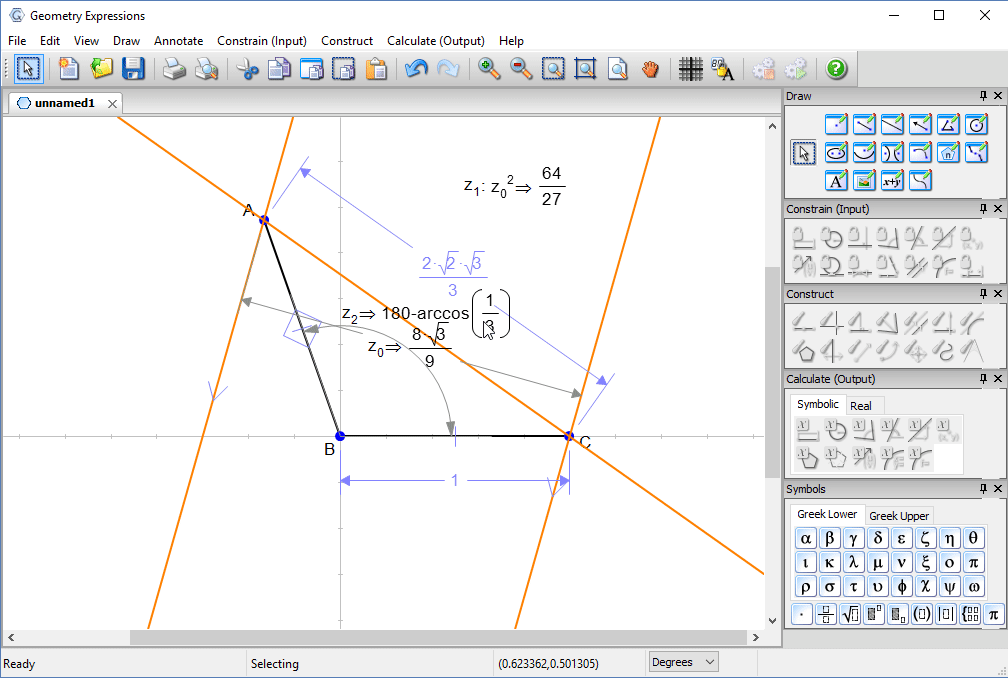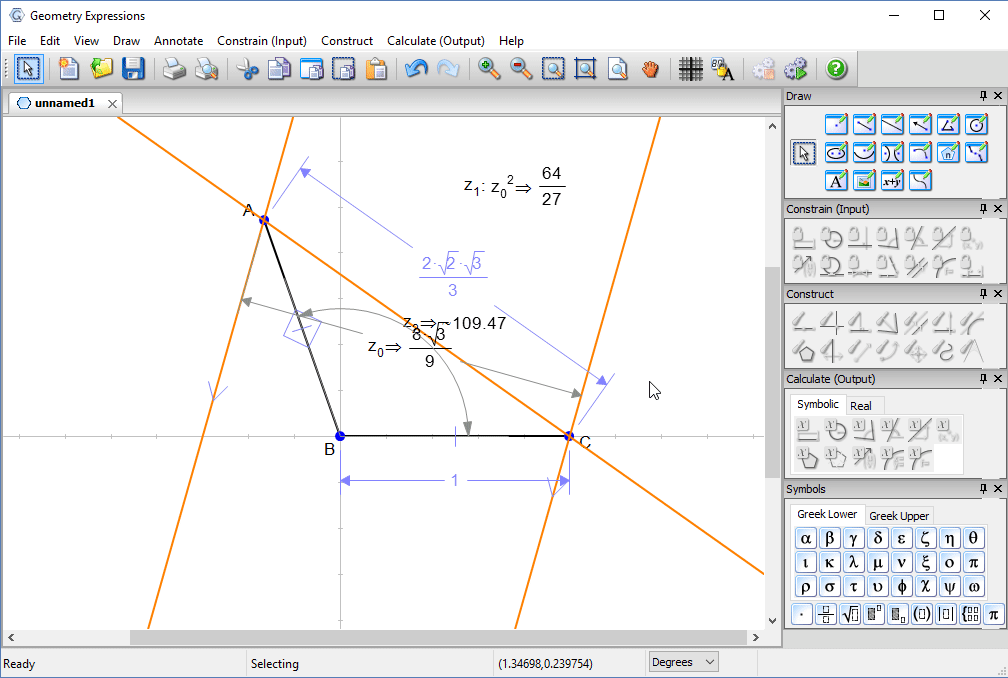
A little simple calculus will give us a value for x at the maximum of sqrt(8/3)
We can replace x with this value and find the maximum width (which is in fact the maximum solar concentration ratio.
We can also determine the lid angle.
Have you ever seen that angle before?