Caustic
We model the curve formed by light reflecting in the walls of a cylinder.
We assume a point light source somewhere inside the cylinder and ask the question, where does the cusp in the caustic lie?

We model the curve formed by light reflecting in the walls of a cylinder.
We assume a point light source somewhere inside the cylinder and ask the question, where does the cusp in the caustic lie?
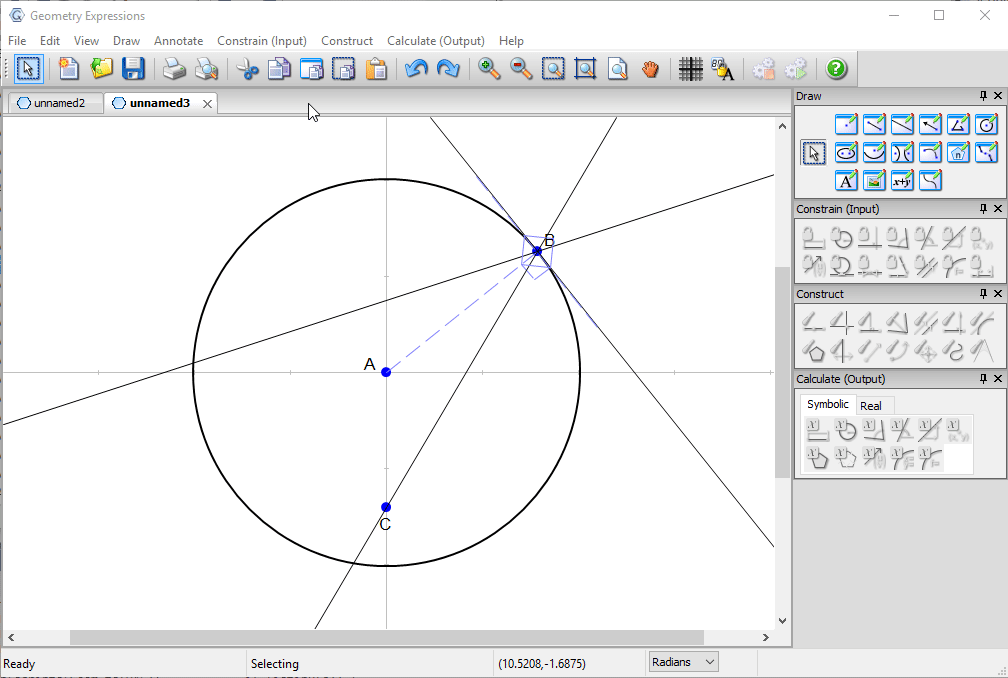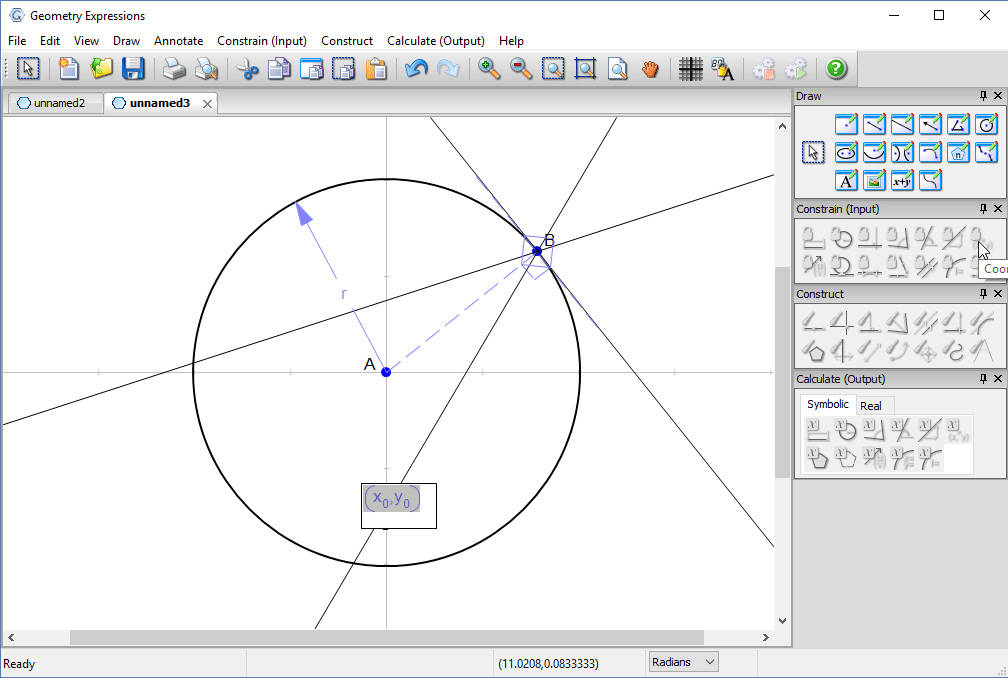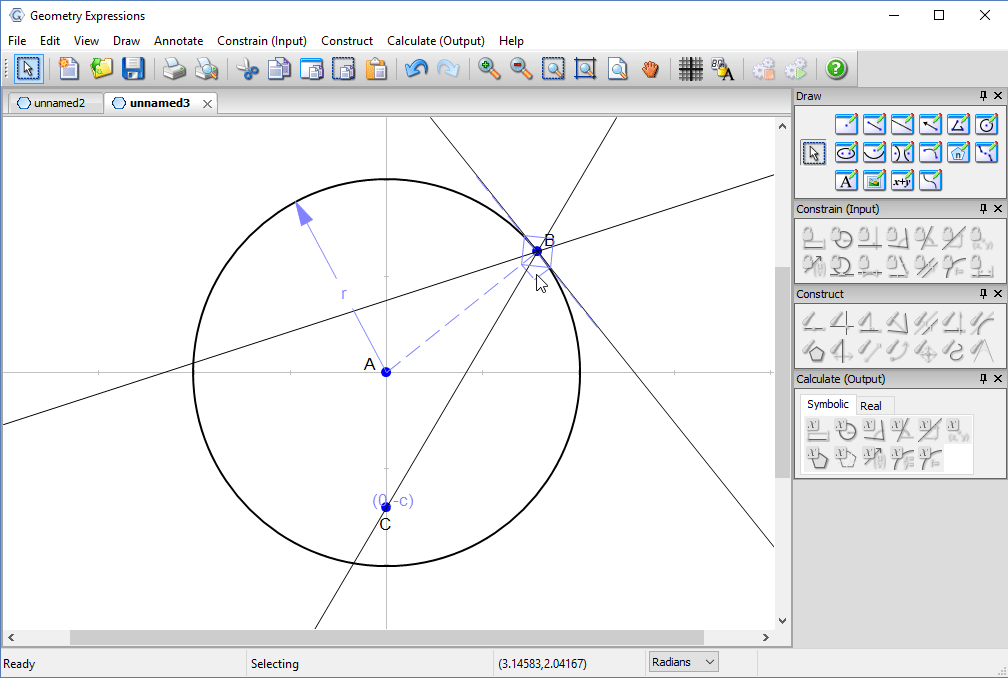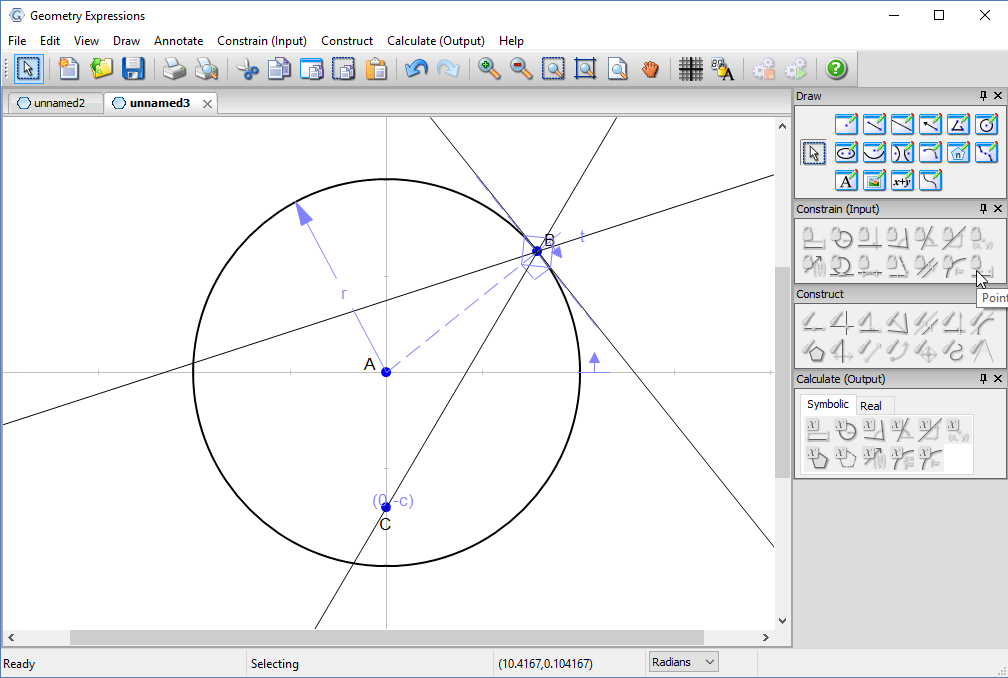
Our mathematical model will consist of a circle centered at the origin, a point B on its circumference and a point C which represents the light source.
A ray from C to B will be reflected in the tangent to the circle at B.
We constrain our model, first specifying the radius of the circle and the location of point C.
We then constrain the parametric location of B on the circle (effectively its angle in radians counter-clockwise from the x-axis) to be t.
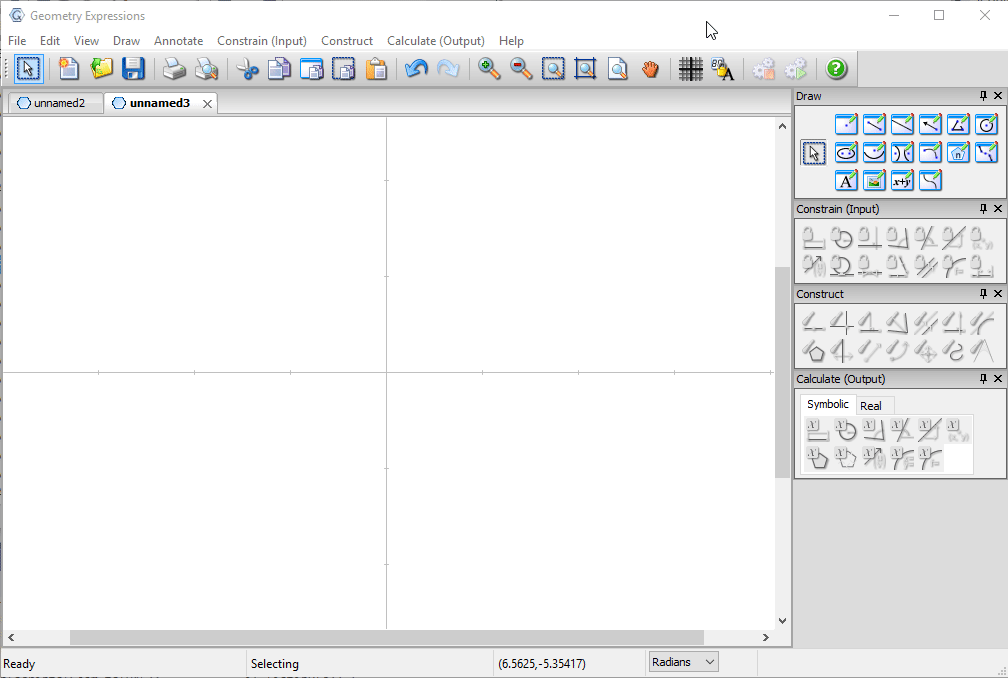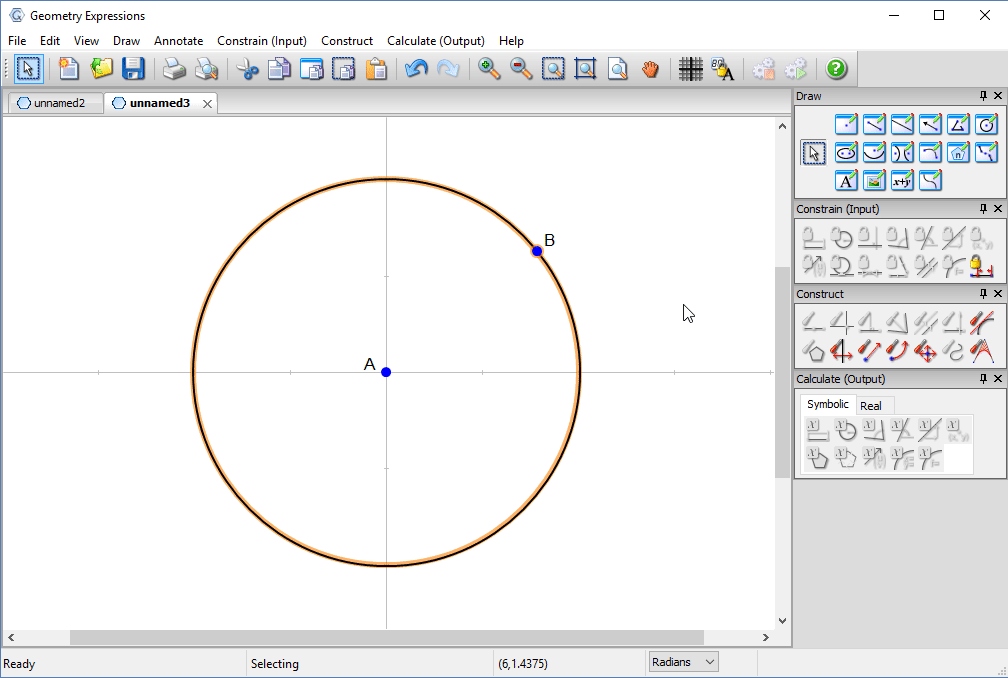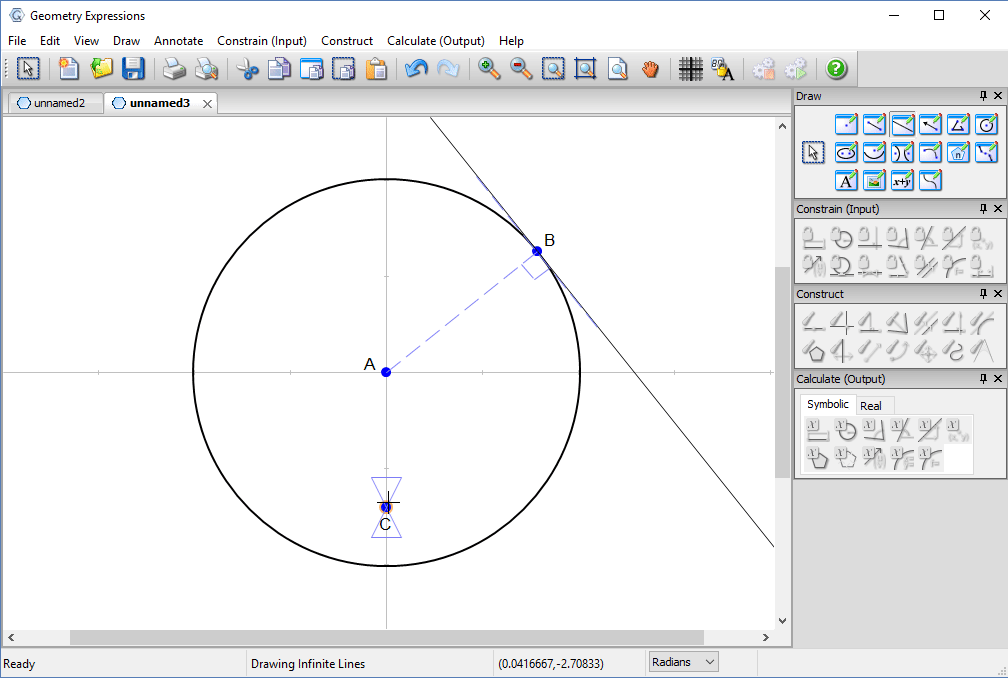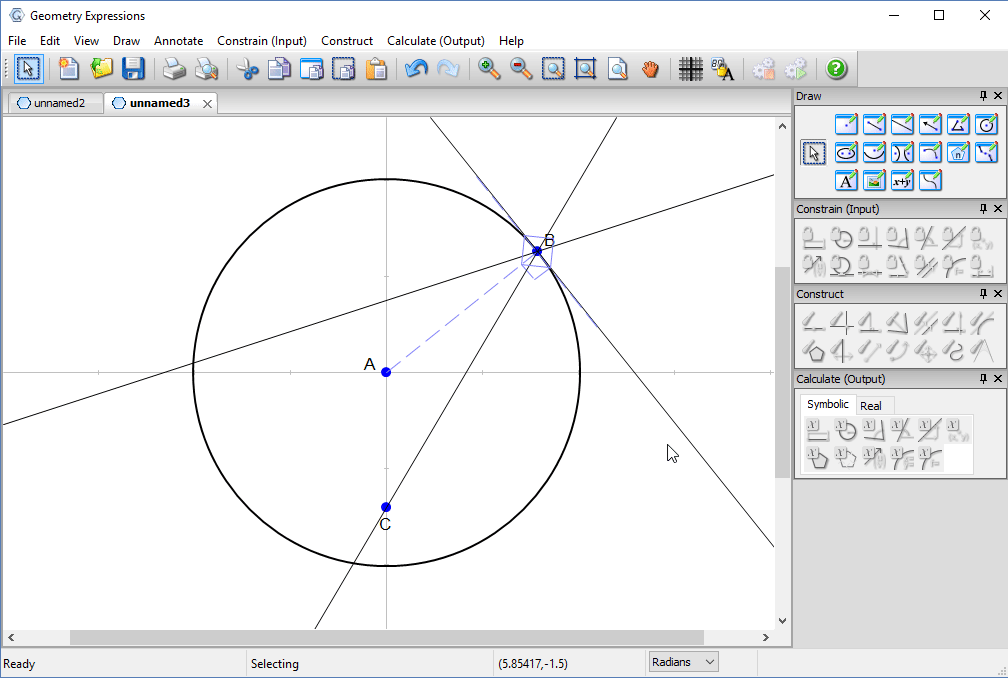
We create a trace to see the family of reflected lines as t varies around the circle.
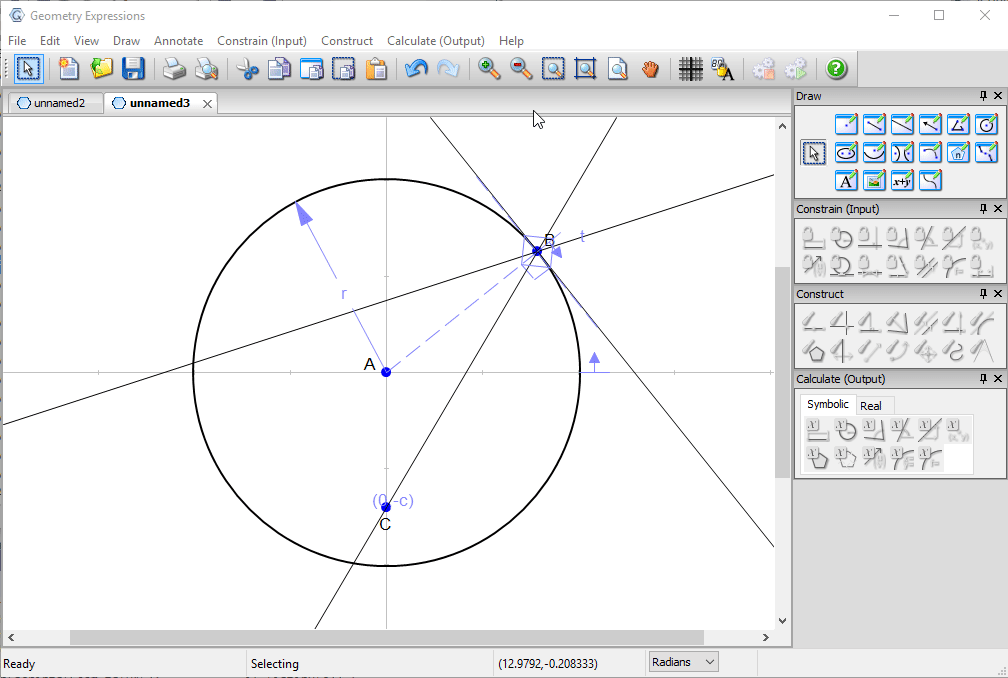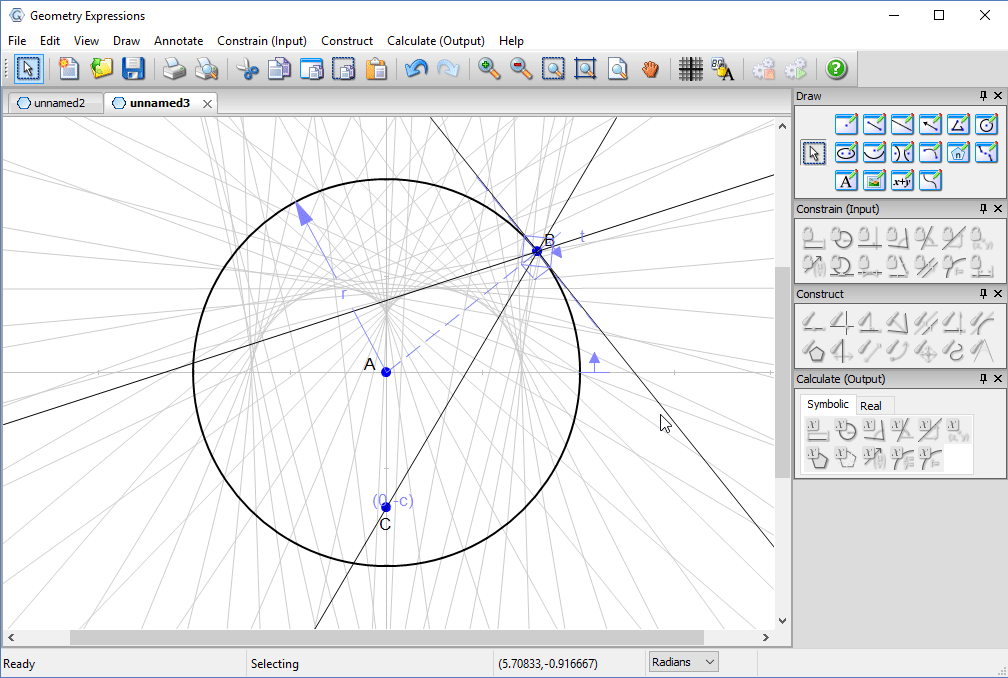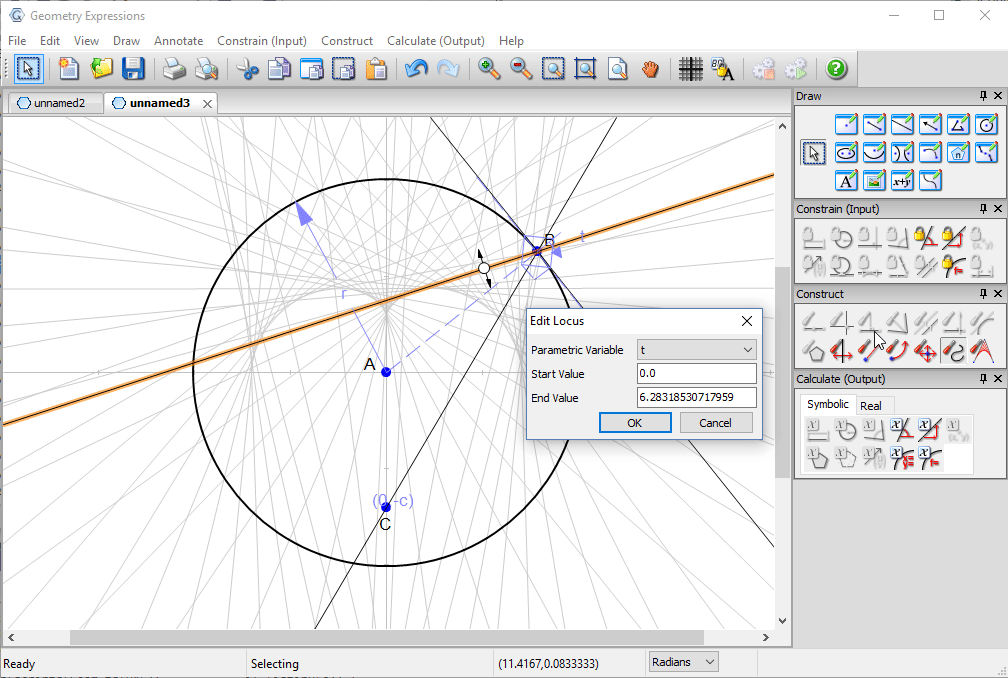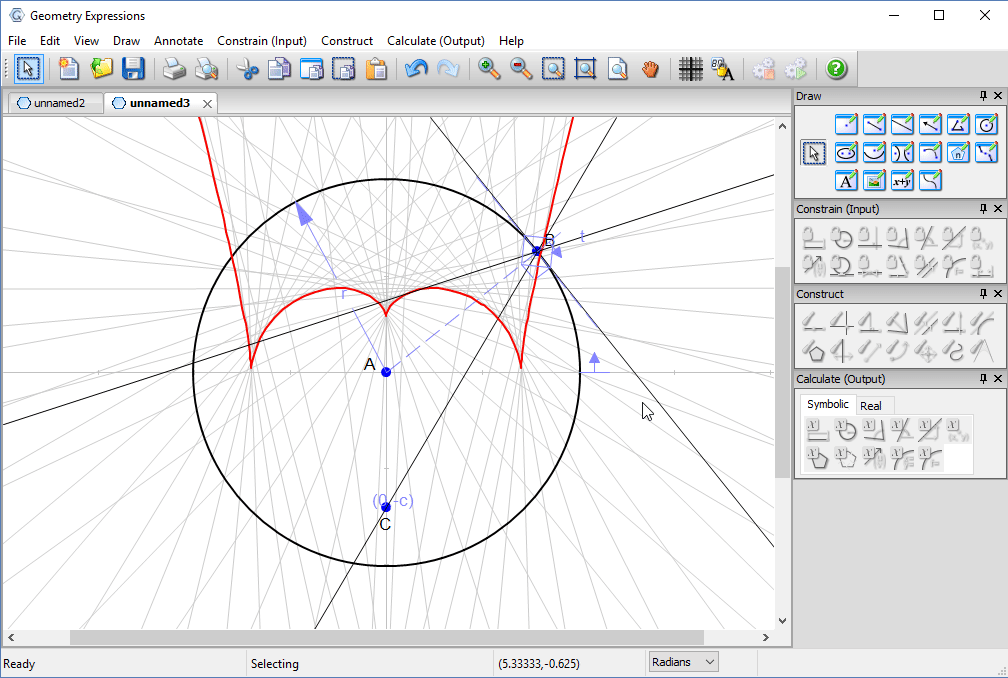
Using the locus tool we create the envelope of the reflected line. This is the curve to which the entire family is tangent, and is the caustic curve observed in the picture.
Animating t lets us observe the relation betwee the reflected lines and the curve.
We also observe that the cusp occurs when both projected ray and reflected ray are vertical.
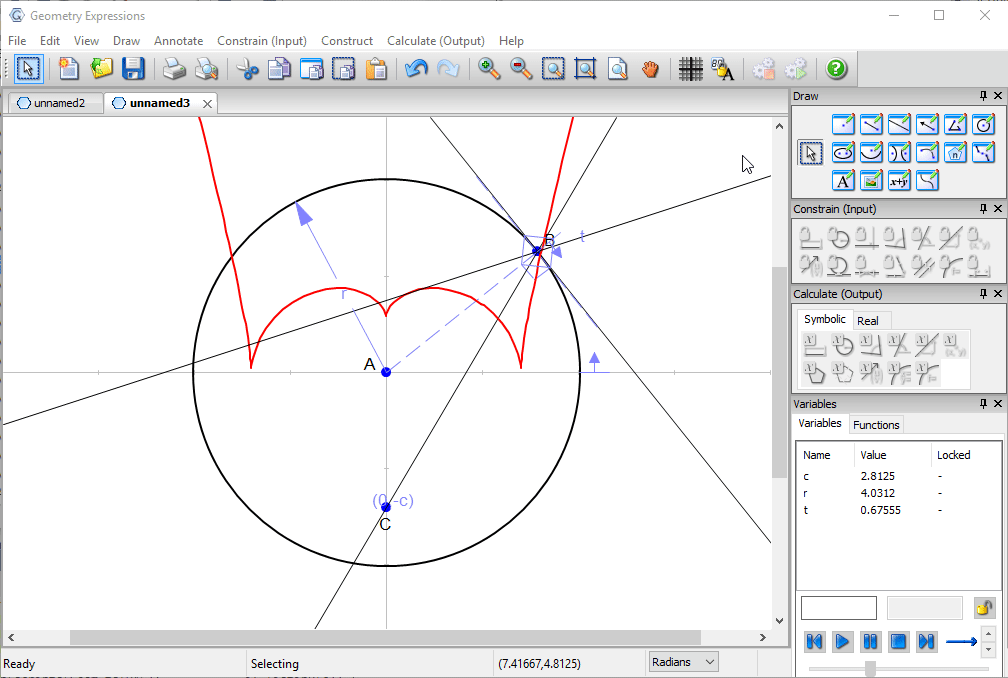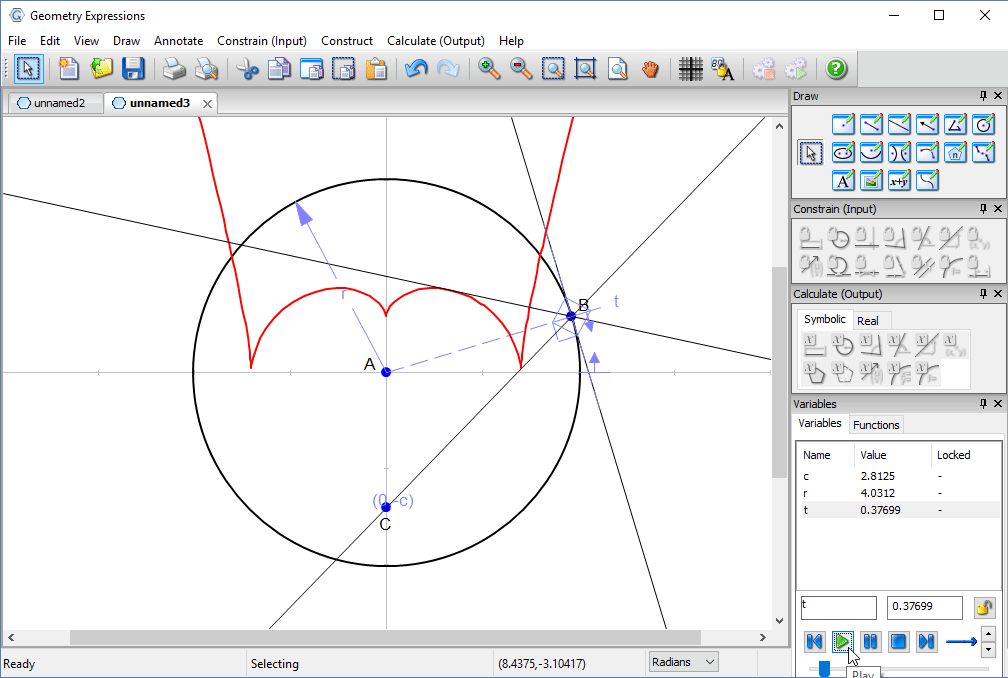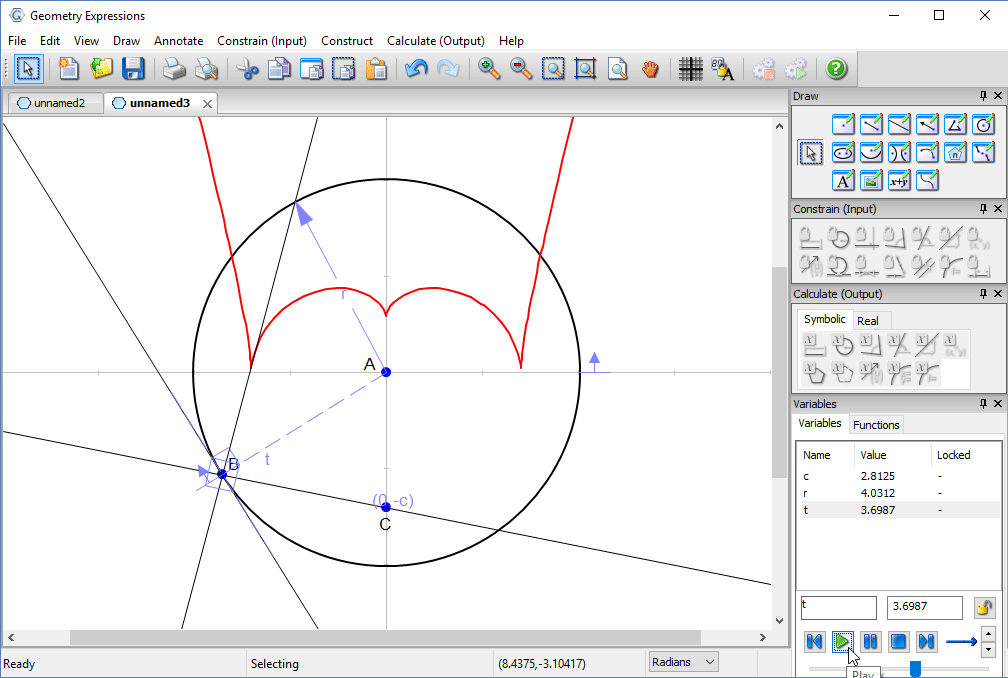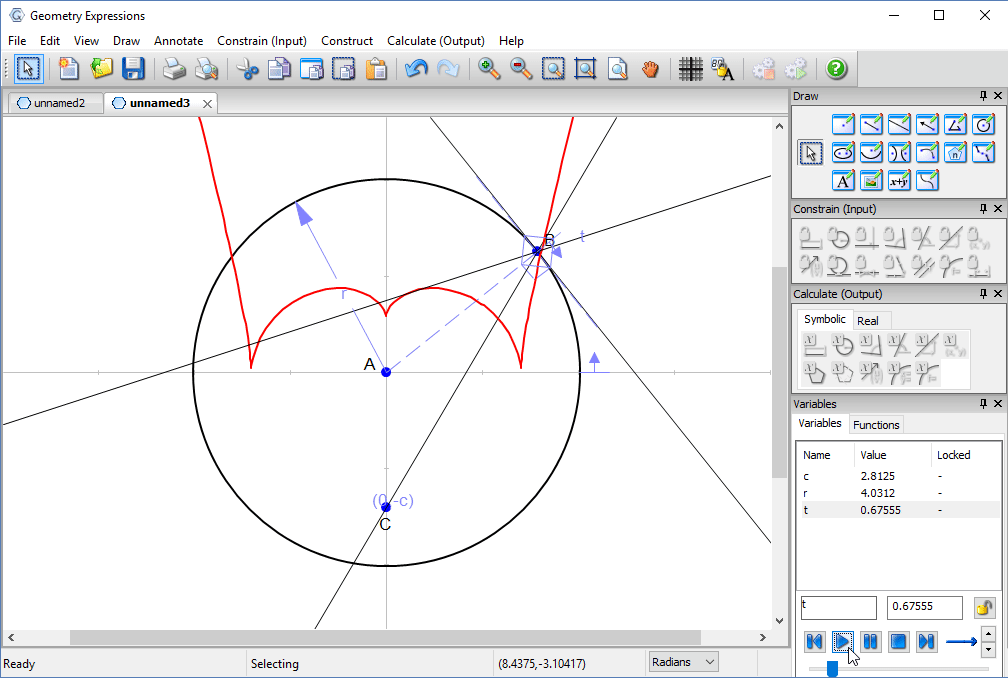
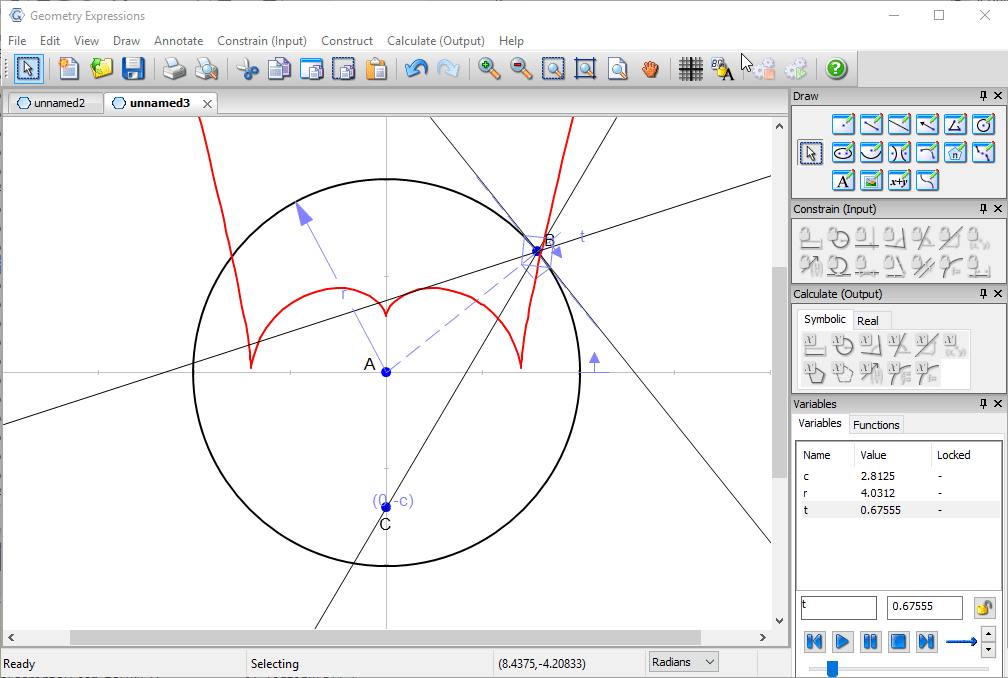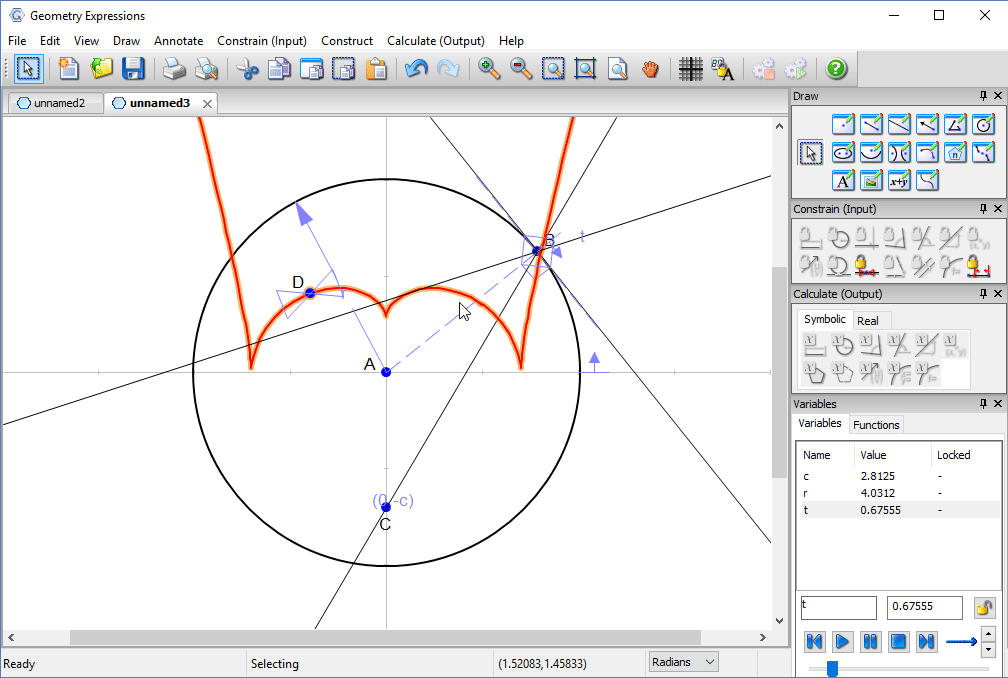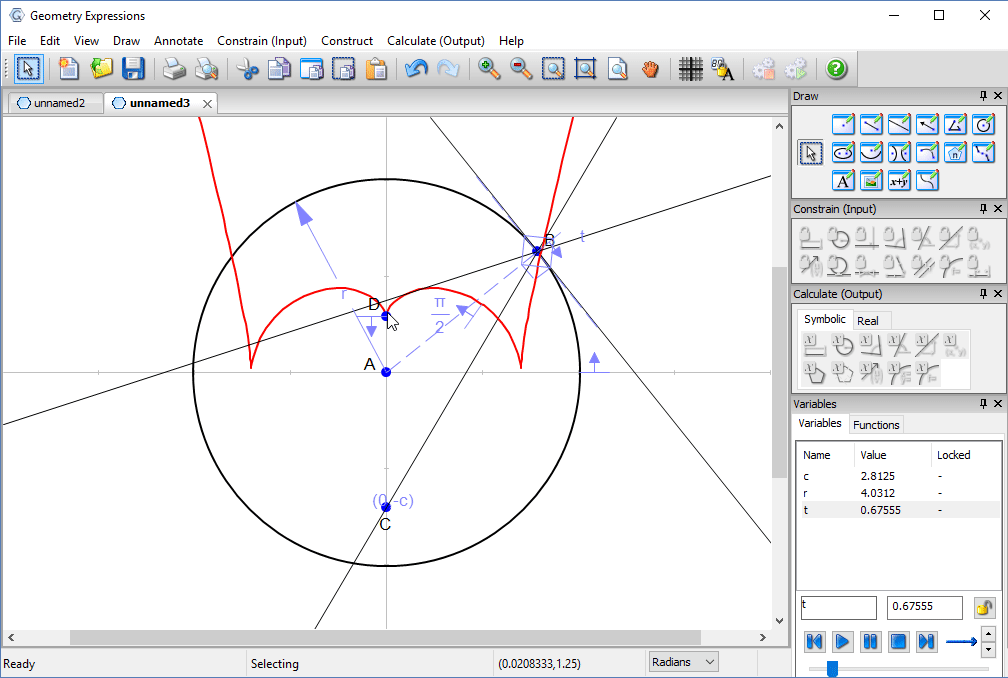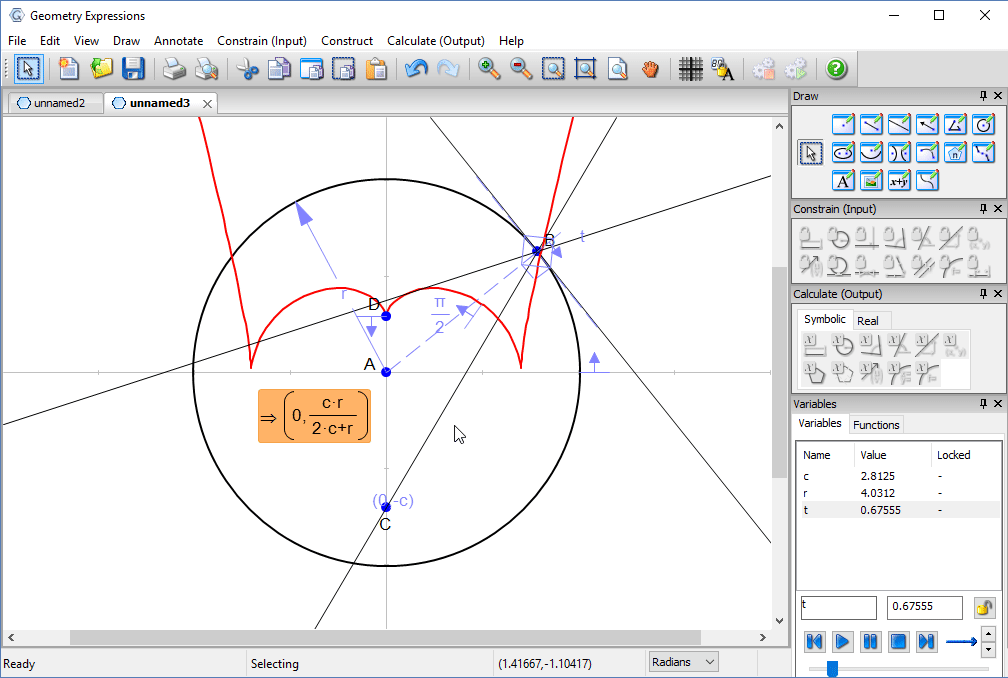
Putting a point on the curve at parametric location π/2, we can measure its coordinates to derive the location of the cusp in terms of the location of the light source.