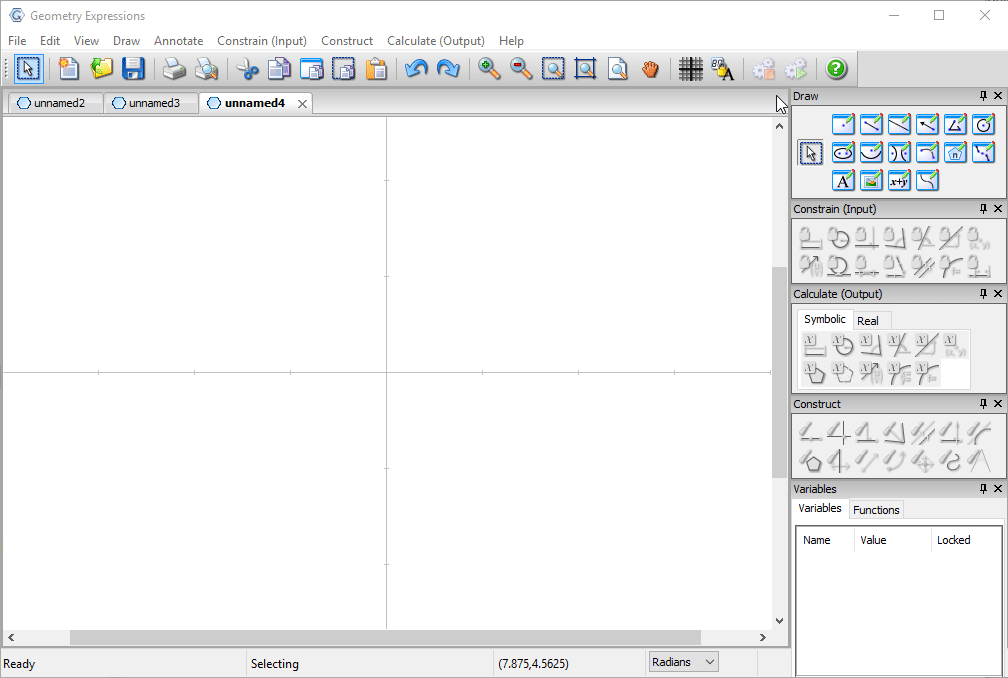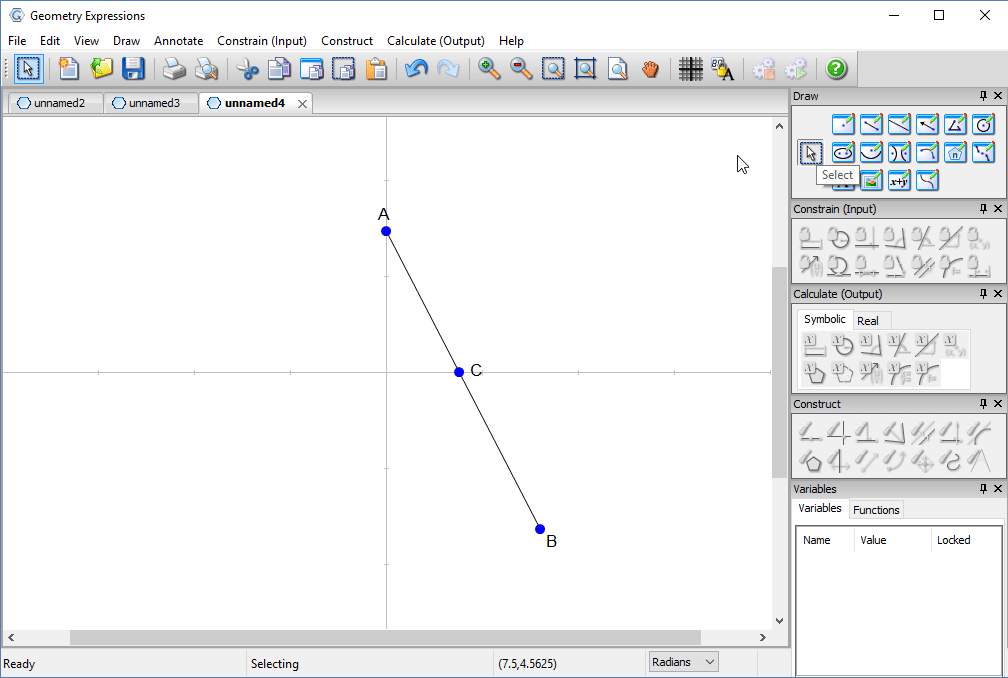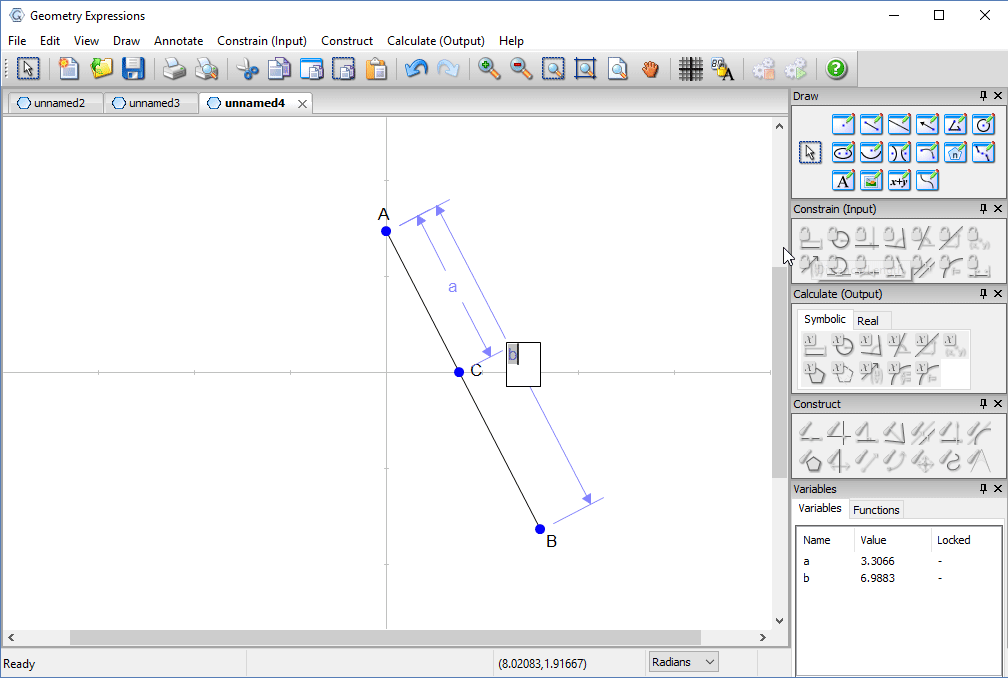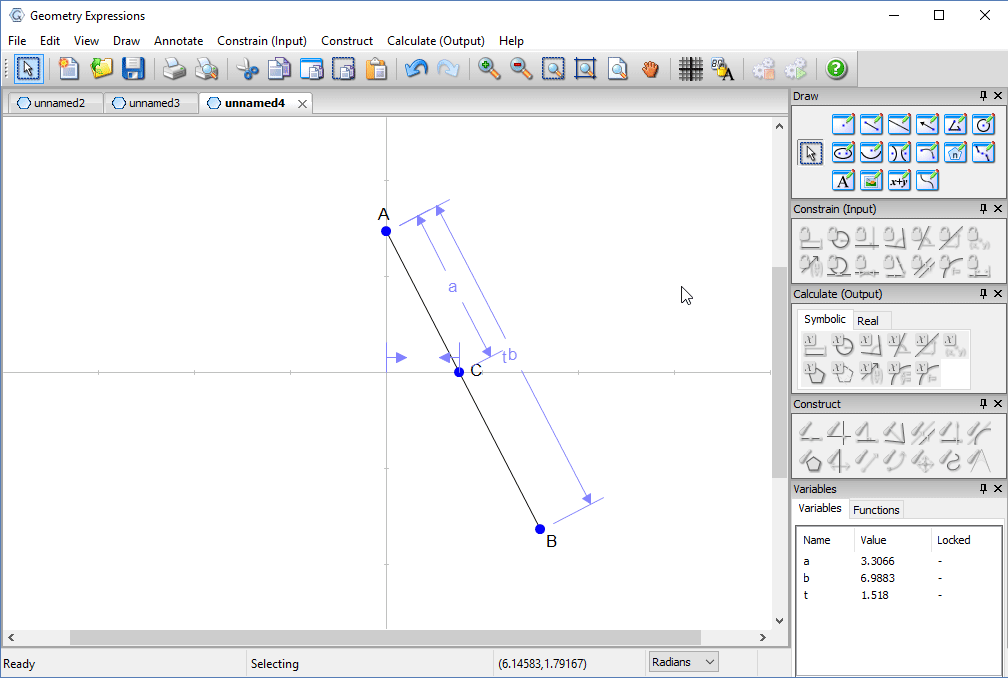
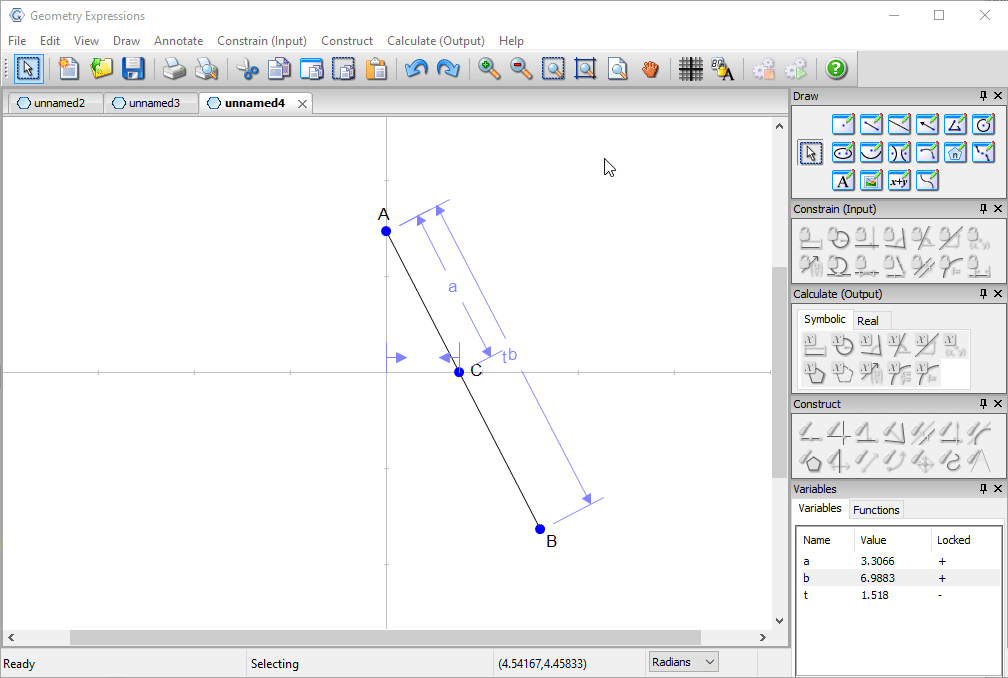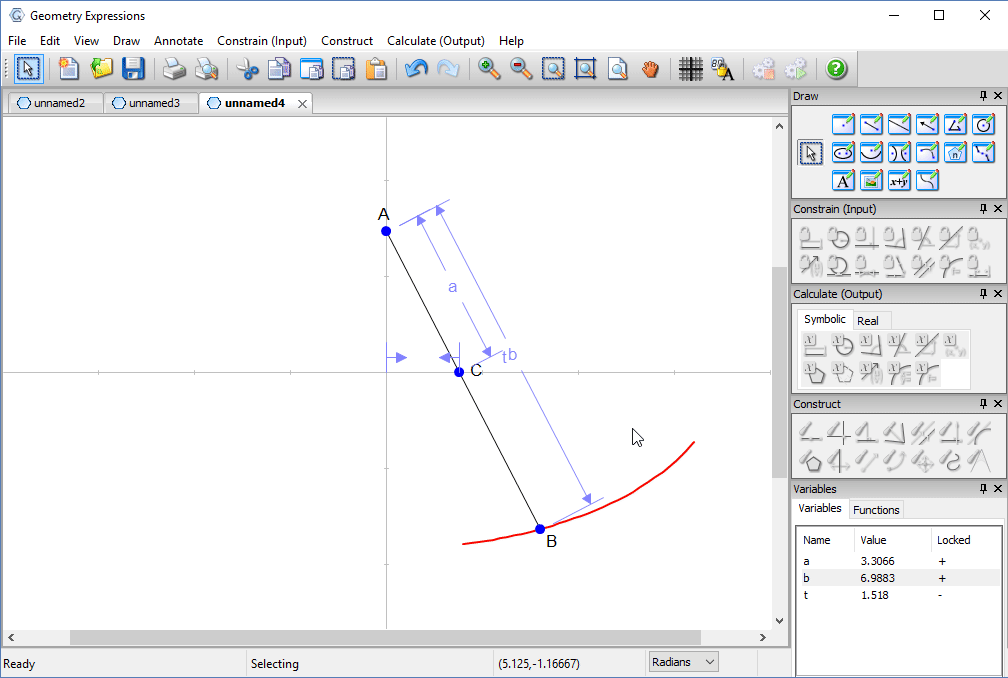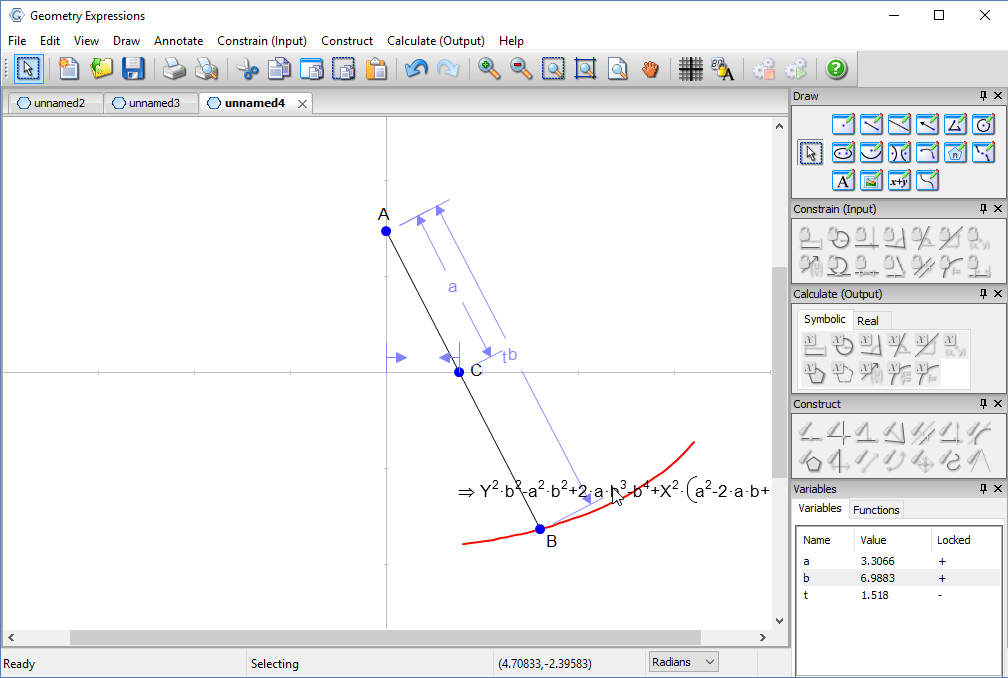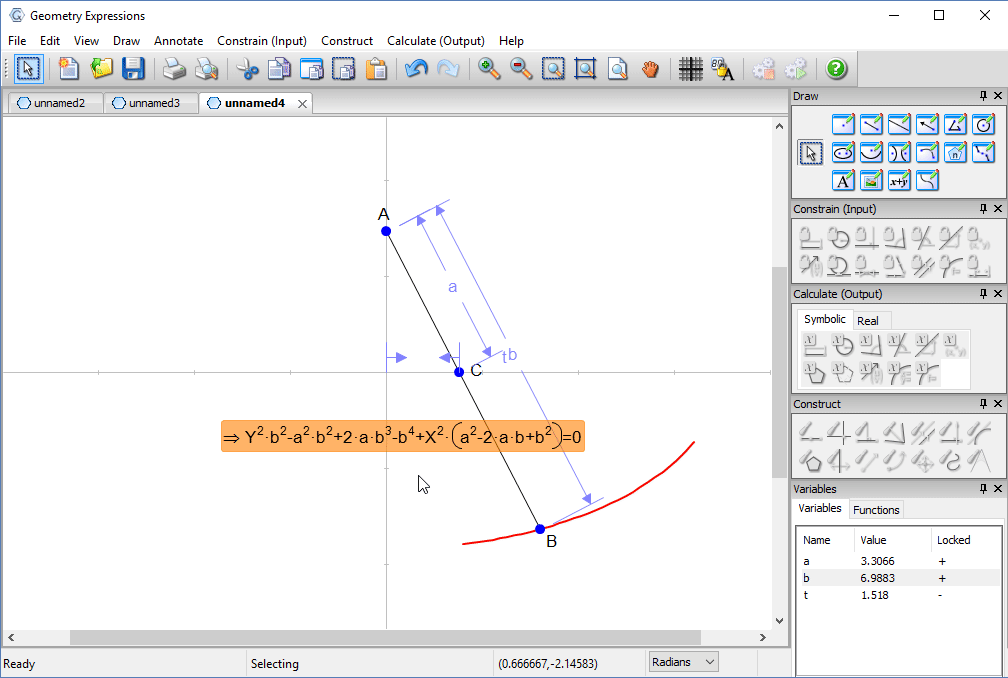
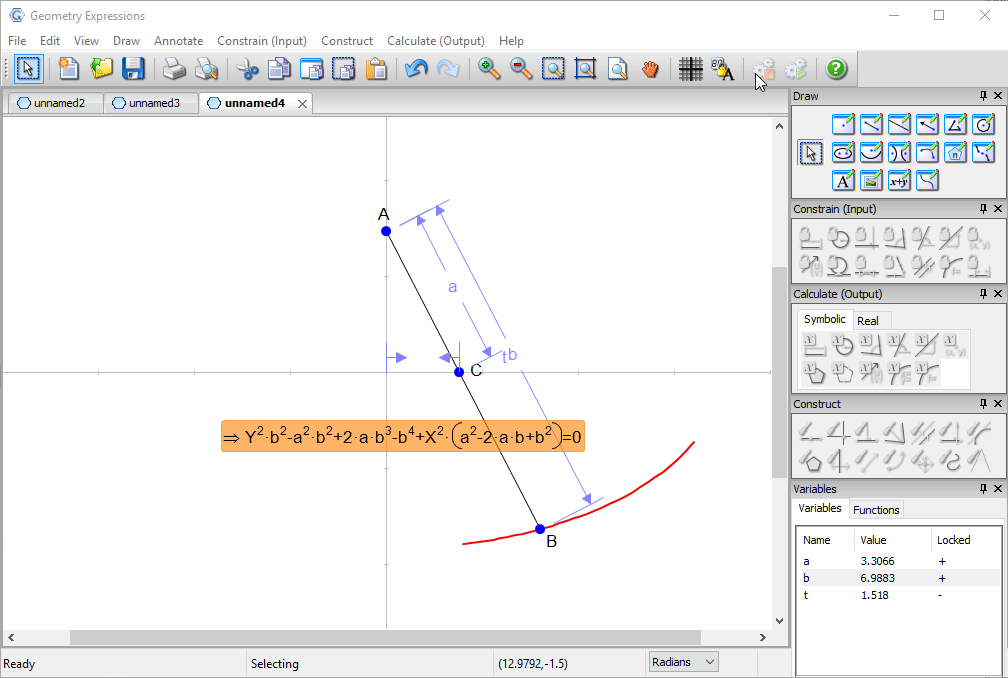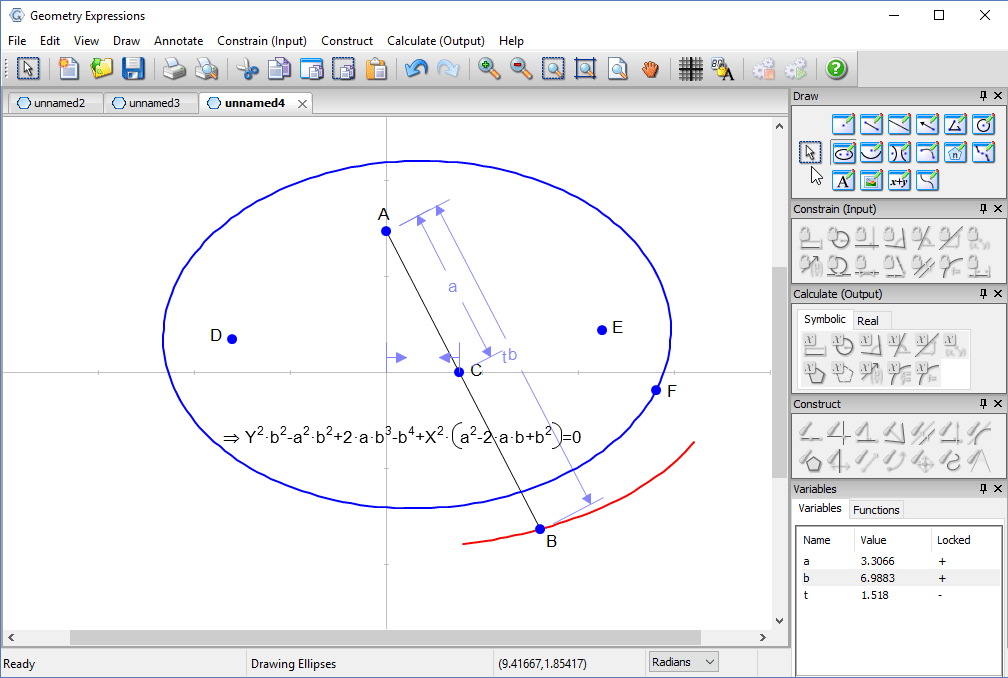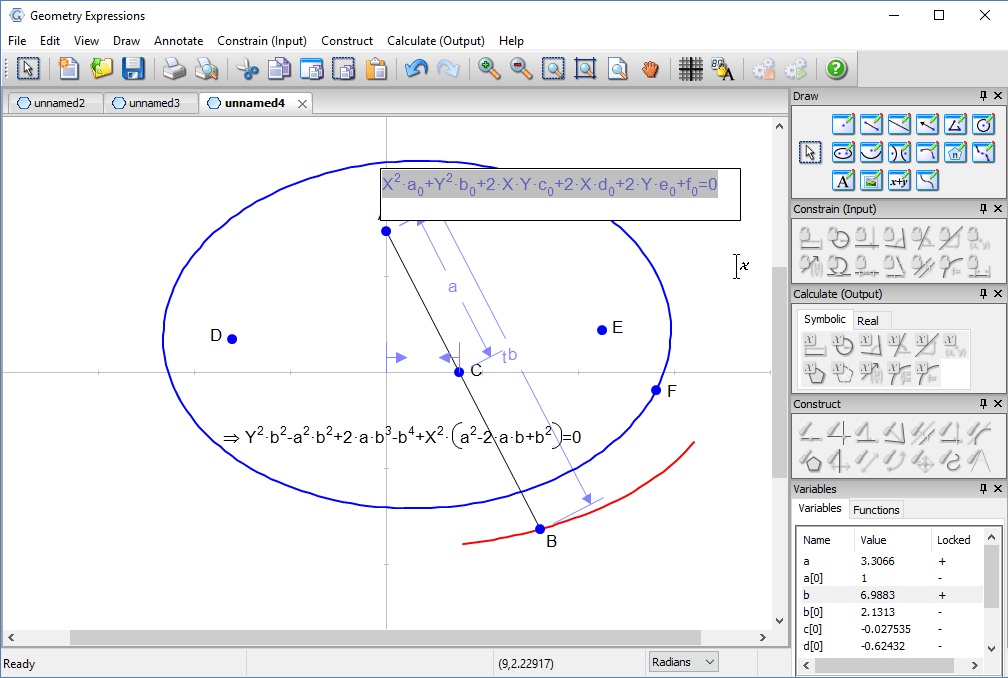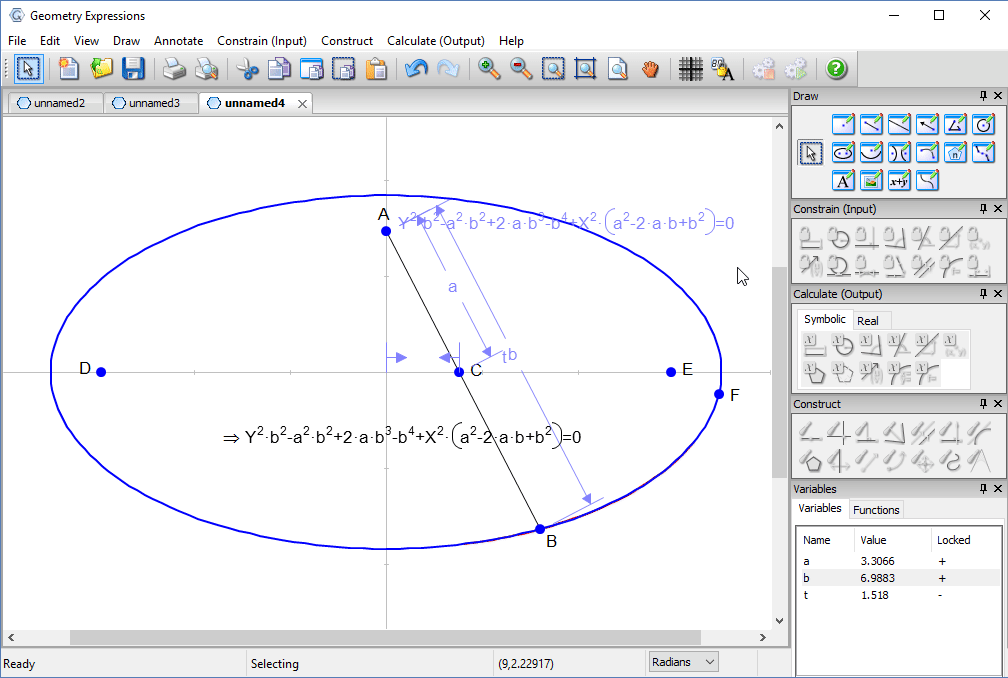
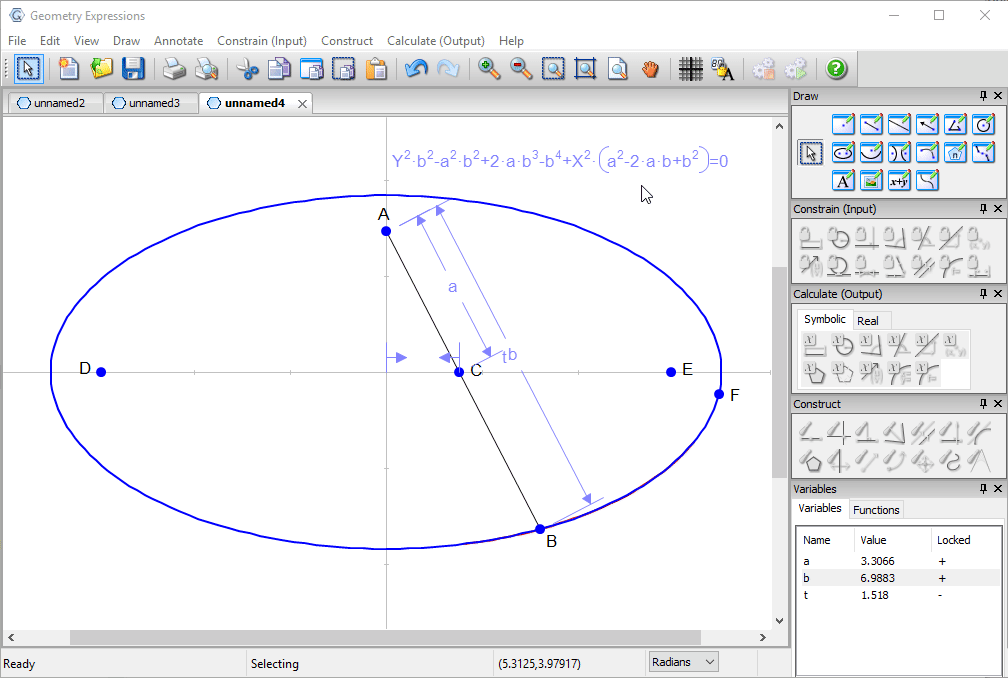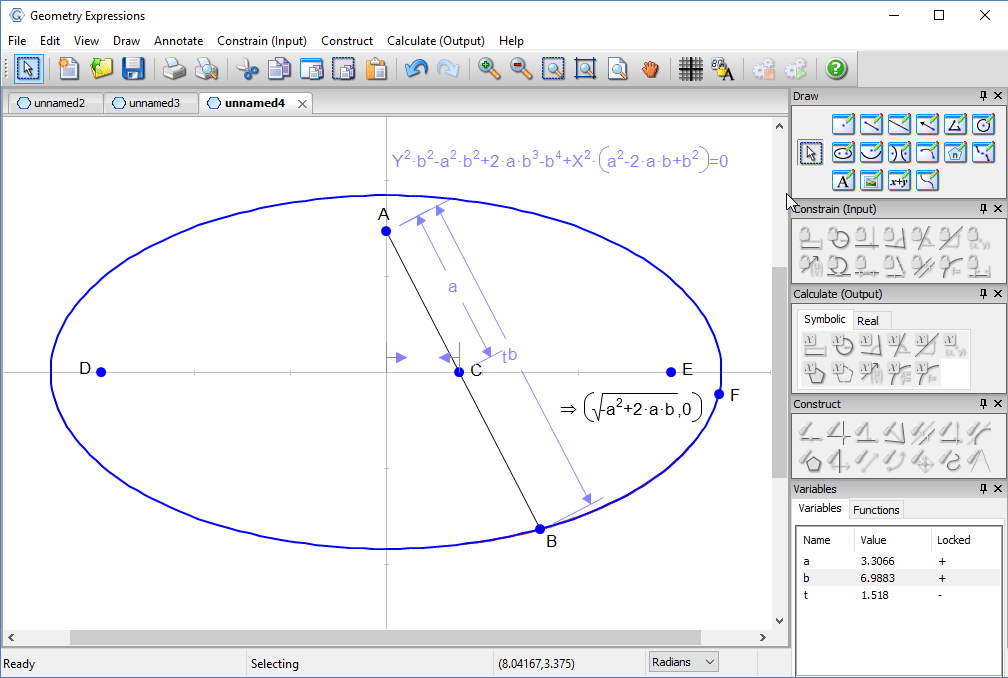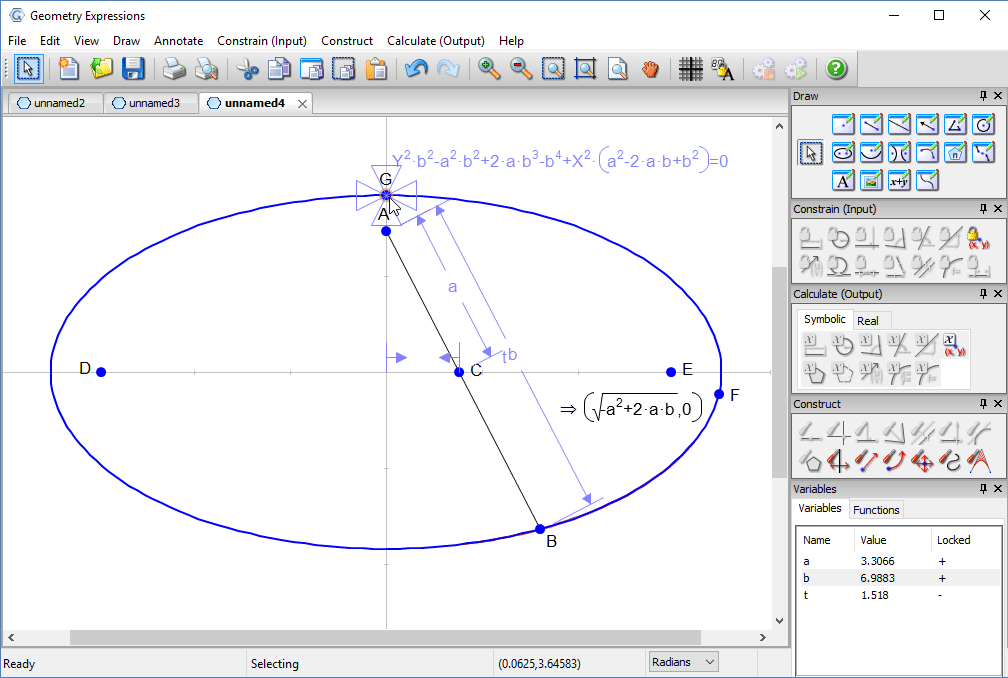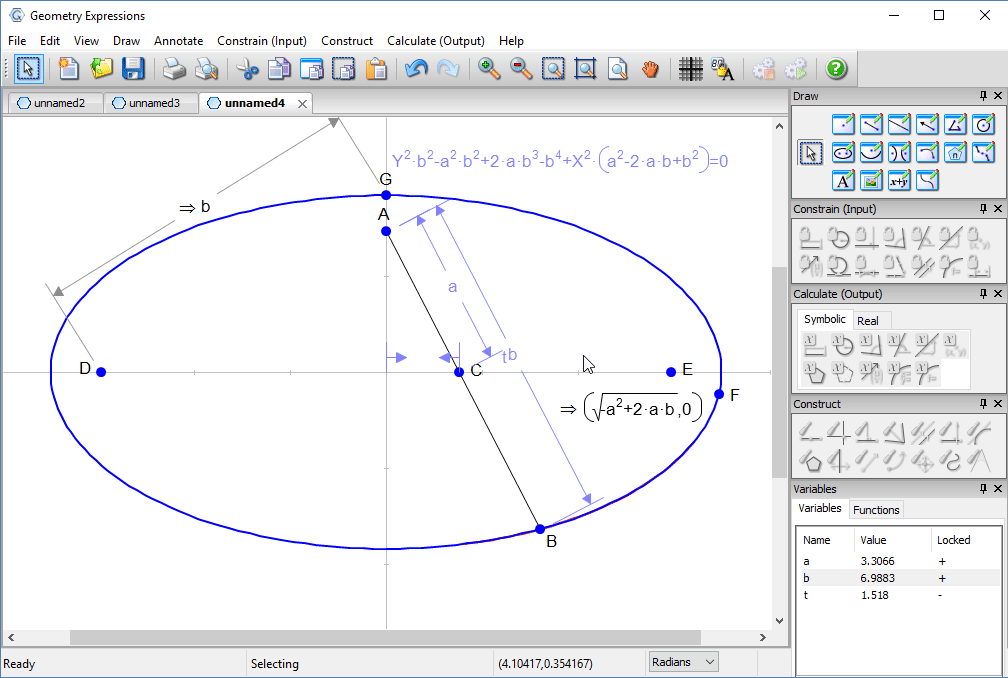
Trammel
Archimedes trammel is a simple device for drawing an ellipse. Another way to draw an ellipse uses a piece of string and two pins.
To match the ellipse drawn by a particular trammel, how long should the string be, and where should the pins go?